题目内容
12.已知函数f(x)=alnx+x2(a为实常数).(1)若函数f(x)在(1,+∞)上是增函数,求a的取值范围;
(2)求函数f(x)在[1,e]上的最小值;
(3)若存在x∈[1,e],使得f(x)≤(a+2)x成立,求实数a的取值范围.
分析 (1)求得函数的导数,由题意可得x>1时,导数f′(x)≥0恒成立,由恒成立思想即可得到所求a的范围;
(2)求出导数,对a讨论,当a≥-2时,当-2e2<a<-2时,当a≤-2e2时,判断导数符号,得到单调性,可得最小值;
(3)由题意可得$a≥\frac{{{x^2}-2x}}{x-lnx}$(x∈[1,e]),由于导数判断右边函数的单调性,即可得到最小值,进而得到a的范围.
解答 解.(1)∵f(x)=x2+alnx,
∴$f'(x)=2x+\frac{a}{x}=\frac{{2{x^2}+a}}{x}$,
由题意x∈(1,+∞),$f'(x)=\frac{{2{x^2}+a}}{x}≥0$恒成立,
即2x2+a≥0对x∈(1,+∞)恒成立,
故a≥-2;
(2)$f'(x)=\frac{{2{x^2}+a}}{x}(x>0)$,当x∈[1,e],2x2+a∈[a+2,a+2e2],
①若a≥-2,f'(x)在[1,e]上非负(仅当a=-2,x=1时,f'(x)=0),
故函数f(x)在[1,e]上是增函数,此时[f(x)]min=f(1)=1.
②若-2e2<a<-2,当$x=\sqrt{\frac{-a}{2}}$时,f'(x)=0;
当$1≤x<\sqrt{\frac{-a}{2}}$时,f'(x)<0,此时f(x)是减函数;
当$\sqrt{\frac{-a}{2}}<x≤e$时,f'(x)>0,此时f(x)是增函数.
故[f(x)]min=$f(\sqrt{\frac{-a}{2}})$=$\frac{a}{2}ln(-\frac{a}{2})-\frac{a}{2}$.
③若a≤-2e2,f'(x)在[1,e]上非正(仅当a=-2e2,x=e时,f'(x)=0),
故函数f(x)在[1,e]上是减函数,此时[f(x)]min=f(e)=a+e2.
综上可知,当a≥-2时,f(x)的最小值为1;
当-2e2<a<-2时,f(x)的最小值为$\frac{a}{2}ln(-\frac{a}{2})-\frac{a}{2}$;
当a≤-2e2时,f(x)的最小值为a+e2;
(3)不等式f(x)≤(a+2)x,可化为a(x-lnx)≥x2-2x.
∵x∈[1,e],∴lnx≤1≤x且等号不能同时取,
∴lnx<x,即x-lnx>0,
因而$a≥\frac{{{x^2}-2x}}{x-lnx}$(x∈[1,e]),
令$g(x)=\frac{{{x^2}-2x}}{x-lnx}$(x∈[1,e]),又$g'(x)=\frac{(x-1)(x+2-2lnx)}{{{{(x-lnx)}^2}}}$,
当x∈[1,e]时,x-1≥0,lnx≤1,x+2-2lnx>0,
从而g'(x)≥0(仅当x=1时取等号),即g(x)在[1,e]上为增函数,
故g(x)的最小值为g(1)=-1,
则a的取值范围是[-1,+∞).
点评 本题考查导数的运用:求单调性和最值,同时考查不等式恒成立问题的解法,注意运用参数分离和构造函数,求得单调性,求得最值,考查运算能力,属于中档题.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案| 人数 | 管理 | 技术开发 | 营销 | 生产 | 共计 |
| 老年 | 40 | 40 | 40 | 80 | 200 |
| 中年 | 80 | 120 | 160 | 240 | 600 |
| 青年 | 40 | 160 | 280 | 720 | 1 200 |
| 小计 | 160 | 320 | 480 | 1 040 | 2 000 |
(2)若要开一个25人的讨论单位发展与薪金调整方面的座谈会,则应怎样抽选出席人?
(3)若要抽取20人调查对广州亚运会举办情况的了解,则应怎样抽样?
| A. | c≥4 | B. | c≥3 | C. | c≥2 | D. | c≥1 |
| A. | (-1,1) | B. | (-∞,-1) | C. | (1,+∞) | D. | (-∞,-1)∪(1,+∞) |
| A. | $\frac{\sqrt{2}}{10}$ | B. | $\frac{3\sqrt{2}}{10}$ | C. | $\frac{-\sqrt{2}}{10}$ | D. | $\frac{-3\sqrt{2}}{10}$ |
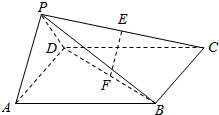 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD,E、F分别为PC、BD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD,E、F分别为PC、BD的中点.