Question

（08年安徽信息交流文）（本小题满分14分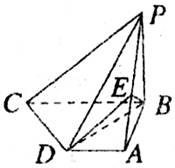）如图，在四棱锥P－ABCD中，PB⊥底面，CD⊥PD，底面ABCD为直角梯形，AD∥BC，AB⊥BC，AB=AD=PB=3，点E在棱PA上，且PE=2EA。

（1）求二面角P－CD－B的正切值；

（2）求异面直线PA与CD所成的角；

（3）求证：PC∥平面EBD。

 

 

 

 

Answer 1

解析:

解法一：

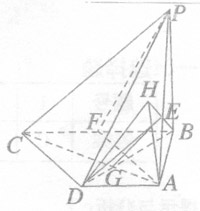（1）由PB⊥面ABCD，CD⊥PD知CD⊥BD

∴就是二面角的平面角，

在直角梯形ABCD中，AD⊥AB，AB=AD=3,

∴BD=，

在中，

    （4分）

（2）由（1）知，CD⊥BD，，∴

取BC的中点F，连结AF，则AF∥CD，∴PA与CD所成的角就是∠PAF

连PF由题设易知AF=PF=PA=，∴∠PAF=60°即为所求         （10分）

（3）连AC交BD于G，连EG，易知,

又∴，∴PC∥EG,又EG面EBD，∴PC∥面EBD  （14分）

EBD，∴PC∥面EBD  （14分）

 

解法二：

    （1）同法一                          （4分）

（2）如图建立空间直角坐标系，设

则A（0,3,0）,P（0,0,3）D（3,3,0）,C（，0，0），

=

∵，∴，

即：3（3-）+9=0         （6分）

∴

∴，∴，

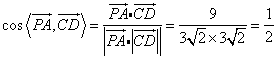即异面直线PA与CD所成的交为60°                            （10分）

（3）同法一                                                     （14分）