题目内容
若椭圆mx2 + ny2 = 1与直线x+y-1=0交于A、B两点,过原点与线段AB中点的直线的斜率为 ,则
,则 =( )
=( )
A. B.
B.  C.
C. D.
D.
B
解析试题分析:设 ,则
,则 ,两式相减,得:
,两式相减,得: ,因为过原点与线段AB中点的直线的斜率为
,因为过原点与线段AB中点的直线的斜率为 ,所以
,所以 ,所以
,所以 。
。
考点:直线与椭圆的综合应用。
点评:在直线与椭圆的综合应用中,当遇到有关弦的斜率和中点问题的时候,常用点差法。利用点差法可以减少很多计算,所以在解有关问题时用这种方法较好。

练习册系列答案
相关题目
已知实数 ,
, ,
, 构成一个等比数列,则圆锥曲线
构成一个等比数列,则圆锥曲线 的离心率为( )
的离心率为( )
A. | B. | C. | D.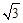 |
若点O和点F分别为双曲线 的中心和左焦点,点P为双曲线右支上的任意一点,则
的中心和左焦点,点P为双曲线右支上的任意一点,则 的最小值为( )
的最小值为( )
| A.-6 | B.-2 | C.0 | D.10 |
抛物线 的准线方程是( )
的准线方程是( )
A. | B. | C. | D. |
已知曲线C:y=2x2,点A(0,-2)及点B(3,a),从点A观察点B,要实现不被曲线C挡住,则实数a的取值范围是( )
| A.(4,+∞) | B.(-∞,4) |
| C.(10,+∞) | D.(-∞,10) |
椭圆 的左焦点为F,右顶点为A,以FA为直径的圆经过椭圆的上顶点,则椭圆的离心率为( )
的左焦点为F,右顶点为A,以FA为直径的圆经过椭圆的上顶点,则椭圆的离心率为( )
A.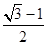 | B. | C. | D. |
以 为中心,
为中心,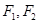 为两个焦点的椭圆上存在一点
为两个焦点的椭圆上存在一点 ,满足
,满足 ,则该椭圆的离心率为
,则该椭圆的离心率为
A. | B. | C. | D. |




 和-1,则点C所对应的实数是
和-1,则点C所对应的实数是