题目内容
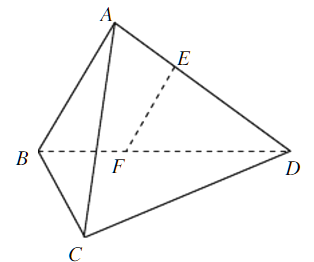
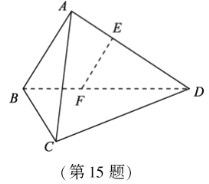
【题目】如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.
求证:(1)EF∥平面ABC;
(2)AD⊥AC.
【答案】(1)在平面![]() 内,AB⊥AD,
内,AB⊥AD,![]() ,则
,则![]() .∵
.∵![]() 平面ABC,
平面ABC,![]() 平面ABC,∴EF∥平面ABC.
平面ABC,∴EF∥平面ABC.
(2)∵BC⊥BD,平面![]() 平面BCD=BD,平面ABD⊥平面BCD,
平面BCD=BD,平面ABD⊥平面BCD,![]() 平面BCD,∴
平面BCD,∴![]() 平面
平面![]() .∵
.∵![]() 平面
平面![]() ,∴
,∴![]()
![]() .∵AB⊥AD,
.∵AB⊥AD,![]() 平面ABC,
平面ABC,![]() ,∴AD⊥平面ABC,又AC
,∴AD⊥平面ABC,又AC![]() 平面ABC,∴AD⊥AC.
平面ABC,∴AD⊥AC.
【解析】
证明:(1)在平面![]() 内,因为AB⊥AD,
内,因为AB⊥AD,![]() ,所以
,所以![]() .
.
 又因为
又因为![]() 平面ABC,
平面ABC,![]() 平面ABC,所以EF∥平面ABC.
平面ABC,所以EF∥平面ABC.
(2)因为平面ABD⊥平面BCD,
平面![]() 平面BCD=BD,
平面BCD=BD,
![]() 平面BCD,
平面BCD,![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]()
![]() .
.
又AB⊥AD,![]() ,
,![]() 平面ABC,
平面ABC,![]() 平面ABC,
平面ABC,
所以AD⊥平面ABC,
又因为AC![]() 平面ABC,
平面ABC,
所以AD⊥AC.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案【题目】拖延症总是表现在各种小事上,但日积月累,特别影响个人发展.某校的一个社会实践调查小组,在对该校学生进行“是否有明显拖延症”的调查中,随机发放了110份问卷.对收回的100份有效问卷进行统计,得到如下![]() 列联表:
列联表:
有明显拖延症 | 无明显拖延症 | 合计 | |
男 | 35 | 25 | 60 |
女 | 30 | 10 | 40 |
合计 | 65 | 35 | 100 |
(Ⅰ)按女生是否有明显拖延症进行分层,已经从40份女生问卷中抽取了8份问卷,现从这8份问卷中再随机抽取3份,并记其中无明显拖延症的问卷的份数为![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)若在犯错误的概率不超过![]() 的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的
的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
