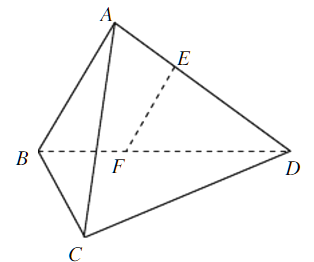
题目内容
【题目】已知椭圆![]() :
: ![]() (
(![]() )的上、下两个焦点分别为
)的上、下两个焦点分别为![]() ,
, ![]() ,过
,过![]() 的直线交椭圆于
的直线交椭圆于![]() ,
, ![]() 两点,且
两点,且![]() 的周长为8,椭圆
的周长为8,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() 为坐标原点,直线
为坐标原点,直线![]() :
: ![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,点
有且仅有一个公共点,点![]() ,
, ![]() 是直线
是直线![]() 上的两点,且
上的两点,且![]() ,
, ![]() ,求四边形
,求四边形![]() 面积
面积![]() 的最大值.
的最大值.
【答案】(1)![]() .(2)4.
.(2)4.
【解析】试题分析:(1)首先根据椭圆中焦点三角形周长结论可得![]() ,,然后由
,,然后由![]() ,即可得椭圆的基本量求解方程(2)直线与椭圆只有一个交点,则联立后方程
,即可得椭圆的基本量求解方程(2)直线与椭圆只有一个交点,则联立后方程![]() =0得m,k的关系式,然后由点到直线距离公式得d1,d2,写出四边形
=0得m,k的关系式,然后由点到直线距离公式得d1,d2,写出四边形![]() 的面积
的面积![]() ,将各量代入化简求解即可
,将各量代入化简求解即可
试题解析:
(1)因为![]() 的周长为8,所以
的周长为8,所以![]() ,所以
,所以![]() .又因为
.又因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)将直线![]() 的方程
的方程![]() 代入到椭圆方程
代入到椭圆方程![]() 中,得
中,得![]()
![]() .
.
由直线与椭圆仅有一个公共点,知![]()
![]() ,化简得
,化简得![]() .
.
设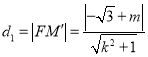 ,
, 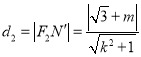 ,
,
所以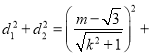
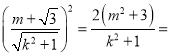
![]() ,
,
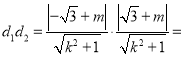
![]() ,
,
所以![]()
![]()
![]() .
.
因为四边形![]() 的面积
的面积![]() ,
,
所以![]()
![]()
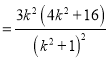 .
.
令![]() (
(![]() ),则
),则
![]()
![]()
![]()
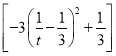 ,
,
所以当![]() 时,
时, ![]() 取得最大值为16,故
取得最大值为16,故![]() ,即四边形
,即四边形![]() 面积的最大值为4.
面积的最大值为4.

练习册系列答案
相关题目