题目内容
【题目】设
,(
)是任意的和为正数的
个不同的实数,(
.)是这个数的一个排列.若对任意的
,有
,则称()是一个“好排列”.求好排列个数的最小值.
【答案】
【解析】
一方面,当
,吨,
均小于0时,易知好排列个数为
.
先证明：好排列个数的最小值就是
对任意满足条件的
.将放在圆周上,而圆排列的个数为.
接下来证明：任意一个圆排列均对应于题设所求的一个好排列,且不同的圆排列对应不同的好排列.
设的一个圆排列为
(约定
.),定义
元好排列(
)满足对任意的
,
,则()为元好排列.
对所有的
,取以
为第一项的好排列
,易知这种好排列是存在的.一个正数就为1元好排列.取好排列中最长的一个,不妨设该好排列的第1项为
,长度为
,即
为好排列.
(l)若
,则结论得证.
(2)若
,则由的最大性知
.
又
,故
.
设
为使
的最小的
,
则
且
均为正数.故(
)为
元好排列.
于是,( ; )为长度大于l的好排列,矛盾.
【注】若()与()有重复项,则去掉中的重复项,同样可以得到长度大于
的好排列.
从而,.
因此,一个圆排列对应一个好排列.又显然不同的圆排列对应不同的好排列.
综上,好排列至少有个.
练习册系列答案
相关题目
【题目】某市的教育主管部门对所管辖的学校进行年终督导评估，为了解某学校师生对学校教学管理的满意度，分别从教师和不同年级的同学中随机抽取若干师生，进行评分(满分100分)，绘制如下频率分布直方图(分组区间为
， 
， 
， 
， 
， 
)，并将分数从低到高分为四个等级：
满意度评分 |
|
|
|
|
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有340人.
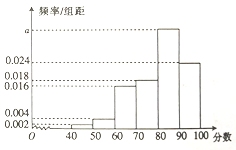
(1)求表中
的值及不满意的人数；
(2)在等级为不满意的师生中，老师占
，现从该等级师生中按分层抽样抽取12人了解不满意的原因，并从中抽取3人担任整改督导员，记
为老师整改督导员的人数，求
的分布列及数学期望.
