题目内容
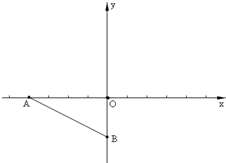 在平面直角坐标系xOy中,已知定点A(-4,0),B(0,-2),半径为r的圆M的圆心M在线段AB的垂直平分线上,且在y轴右侧,圆M被y轴截得的弦长为
在平面直角坐标系xOy中,已知定点A(-4,0),B(0,-2),半径为r的圆M的圆心M在线段AB的垂直平分线上,且在y轴右侧,圆M被y轴截得的弦长为| 3 |
(1)若r为正常数,求圆M的方程;
(2)当r变化时,是否存在定直线l与圆相切?如果存在求出定直线l的方程;如果不存在,请说明理由.
分析:(1)设圆心M(a,b),利用圆心在直线AB的垂直平分线上,从而|MA|=|MB|,再结合圆心在y轴右侧(即a>0),圆M被y轴截得的弦长为
r,列方程组解之即可;
(2)依题意,可设直线l:y=kx+b与圆M相切,利用圆心到直线l的距离等于半径求得m,判断即可.
| 3 |
(2)依题意,可设直线l:y=kx+b与圆M相切,利用圆心到直线l的距离等于半径求得m,判断即可.
解答:解:(1)设圆心M(a,b),由题意可知
,解得
,
所以圆M的方程为(x-
r)2+(y-r-3)2=r2;
(2)
设直线l:y=kx+b,
则
=r对任意r>0恒成立,
由|(
-1)r+b-3|=r
得:
(
-1)2+(k-2)(b-3)r+(b-3)2=(1+k2)r2,
∴
,
解得
或
.
∴存在两条直线y=3和4x+3y-9=0与动圆M均相切.
|
|
所以圆M的方程为(x-
| 1 |
| 2 |
(2)
设直线l:y=kx+b,
则
|k×
| ||
|
由|(
| k |
| 2 |
| 1+k2 |
(
| k |
| 2 |
∴
|
解得
|
|
∴存在两条直线y=3和4x+3y-9=0与动圆M均相切.
点评:本题考查直线与圆的位置关系,考查理解题意与解方程组的能力,属于中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是