题目内容
(2013•金华模拟)已知抛物线y2=4px(p>0)与双曲线
-
=1(a>0,b>0)有相同的焦点F,点A是两曲线的交点,且AF⊥x轴,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
分析:设双曲线的左焦点为F',连接AF',由抛物线方程求得A(p,2p),结合双曲线的焦距,得到△AFF'是以AF'为斜边的等腰直角三角形.再根据双曲线定义,得实轴2a=2p(
-1),而焦距2c=2p,由离心率公式可算出该双曲线的离心率.
| 2 |
解答: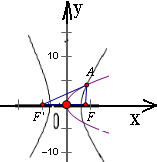 解:设双曲线的左焦点为F',连接AF'
解:设双曲线的左焦点为F',连接AF'
∵F是抛物线y2=4px的焦点,且AF⊥x轴,
∴设A(p,y0),得y02=4p×p,得y0=2p,A(p,2p),
因此,Rt△AFF'中,|AF|=|FF'|=2p,得|AF'|=2
p
∴双曲线
-
=1的焦距2c=|FF'|=2p,实轴2a=|AF'|-|AF|=2p(
-1)
由此可得离心率为:e=
=
=
=
+1
故选:B
 解:设双曲线的左焦点为F',连接AF'
解:设双曲线的左焦点为F',连接AF'∵F是抛物线y2=4px的焦点,且AF⊥x轴,
∴设A(p,y0),得y02=4p×p,得y0=2p,A(p,2p),
因此,Rt△AFF'中,|AF|=|FF'|=2p,得|AF'|=2
| 2 |
∴双曲线
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
由此可得离心率为:e=
| c |
| a |
| 2c |
| 2a |
| 2p | ||
2p(
|
| 2 |
故选:B
点评:本题给出双曲线与抛物线有共同的焦点,求双曲线的离心率,着重考查了双曲线、抛物线的定义与简单几何性质等知识,属于中档题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 (2013•金华模拟)已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则时速在[60,70]的汽车大约有
(2013•金华模拟)已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则时速在[60,70]的汽车大约有