题目内容
【题目】如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF上一点,且DM⊥平面ACE. 
(1)求BM的长;
(2)求二面角A﹣DM﹣B的余弦值的大小.
【答案】
(1)解:设AC∩BD=O,取EF中点N,连接NO
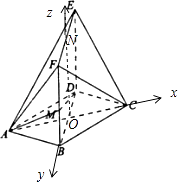
∵四边形ABCD是菱形,∴AC⊥BD,
∵四边形BDEF是矩形,∴ON⊥BD,
∵平面BDEF⊥平面ABCD,平面BDEF∩平面ABCD=BD,ON平面BDEF,
∴ON⊥平面ABCD,
以O为原点,以OC,OB,ON为坐标轴建立空间坐标系如图所示:
∵底面ABCD是边长为2的菱形,∠BAD=60°,
∴OB=OD=1,OA=OC= ![]() ,
,
∵四边形BDEF是矩形,DE=2,
∴A(﹣ ![]() ,0,0),B(0,1,0),C(
,0,0),B(0,1,0),C( ![]() ,0,0),E(0,﹣1,2),D(0,﹣1,0),
,0,0),E(0,﹣1,2),D(0,﹣1,0),
设BM=h,则M(0,1,h),
∴ ![]() =(0,2,h),
=(0,2,h), ![]() =(
=( ![]() ,﹣1,2),
,﹣1,2),
∵DM⊥平面ACE,∴ ![]() ,
,
∴﹣2+2h=0,解得h=1,
∴BM=1
(2)解: ![]() =(
=( ![]() ,﹣1,0),
,﹣1,0), ![]() =(0,2,1),
=(0,2,1),
设平面ADM的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 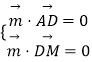 ,
,
∴ ![]() ,令x=
,令x= ![]() 得
得 ![]() =(
=( ![]() ,3,﹣6),
,3,﹣6),
又AC⊥平面BDM,∴ ![]() =(1,0,0)是平面BDM的一个法向量,
=(1,0,0)是平面BDM的一个法向量,
∴cos< ![]() >=
>= ![]() =
= ![]() =
= ![]() ,
,
∴二面角A﹣DM﹣B的余弦值为 ![]()
【解析】(1)建立坐标系,设BM=h,求出 ![]() 和
和 ![]() 的坐标,令
的坐标,令 ![]() =0解出h;(2)求出平面ADM和平面BDM的法向量,计算法向量的夹角即可得出二面角的夹角.
=0解出h;(2)求出平面ADM和平面BDM的法向量,计算法向量的夹角即可得出二面角的夹角.
【考点精析】掌握平面与平面垂直的性质是解答本题的根本,需要知道两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.

