题目内容
16.已知区域T$\left\{{\left.{(x,y)}\right|\left\{\begin{array}{l}x+y≤6\\ 0≤x≤\sqrt{y}\end{array}\right.}\right\}$的面积为t,当x,y∈T时,z=tx-$\frac{11}{3}$y的最大值是( )| A. | -22 | B. | $\frac{11}{3}$ | C. | 0 | D. | $\frac{11}{3}$ |
分析 利用定积分求出t,然后通过线性规划求出z=tx-$\frac{11}{3}$y的最大值.
解答 解:由$\left\{\begin{array}{l}x+y=6\\ x=\sqrt{y}\end{array}\right.$可得x=-3(舍去),x=2,
∴t=${∫}_{0}^{2}(6-x-{x}^{2}){d}_{x}$=$(6x-\frac{1}{2}{x}^{2}-\frac{1}{3}{x}^{3}){|}_{0}^{2}$=$\frac{22}{3}$.
∴z=$\frac{22}{3}$x-$\frac{11}{3}$y,约束条件$\left\{\begin{array}{l}x+y≤6\\ 0≤x≤\sqrt{y}\end{array}\right.$的可行域如图: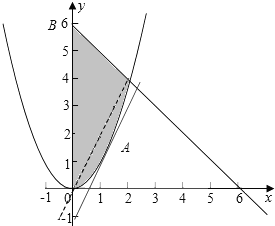
z=$\frac{22}{3}$x-$\frac{11}{3}$y,化为y=2x-$\frac{3}{11}z$,显然y=2x-$\frac{3}{11}z$与y=x2相切时,z取得最大值.
可得2x-$\frac{3}{11}z$=x2,即:x2-2x+$\frac{3}{11}z$=0,△=4-$4×\frac{3}{11}z≥0$,可得z≤$\frac{11}{3}$.
z的最大值为:$\frac{11}{3}$.
故选:B.
点评 本题考查线性规划的应用,画出可行域以及目标函数的几何意义是解题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
4.若x,y满足$\left\{\begin{array}{l}x+y≥0\\ x≥1\\ x-y≥0\end{array}\right.$则下列不等式恒成立的是( )
| A. | y≥1 | B. | x≥2 | C. | x+2y+2≥0 | D. | 2x-y+1≥0 |
11.设i是虚数单位,若复数z(1+i)=1-i满足z(1+i)=1-i,则复数z=( )
| A. | -1 | B. | 1 | C. | i | D. | -i |
6.已知a>b>0,则下列不等关系式中正确的是( )
| A. | sina>sinb | B. | log2a<log2b | C. | a${\;}^{\frac{1}{2}}$<b${\;}^{\frac{1}{2}}$ | D. | ($\frac{1}{3}$)a<($\frac{1}{3}$)b |
 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,过点P(0,1)的动直线l与椭圆交于A,B两点,当l∥x轴时,|AB|=$\frac{4\sqrt{6}}{3}$
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,过点P(0,1)的动直线l与椭圆交于A,B两点,当l∥x轴时,|AB|=$\frac{4\sqrt{6}}{3}$