题目内容
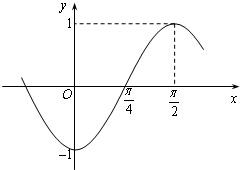 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<π)的图象如图所示.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<π)的图象如图所示.
(Ⅰ)求ω,φ的值;
(Ⅱ)设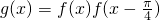 ,求函数g(x)的单调递增区间.
,求函数g(x)的单调递增区间.
解:(Ⅰ)由图可知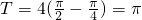 ,
, ,(2分)
,(2分)
又由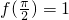 得,sin(π+∅)=1,又f(0)=-1,得sinφ=-1
得,sin(π+∅)=1,又f(0)=-1,得sinφ=-1
∵|∅|<π∴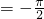 ,(4分)
,(4分)
(Ⅱ)由(Ⅰ)知: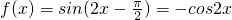 (6分)
(6分)
因为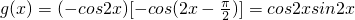 =
=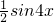 (9分)
(9分)
所以,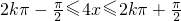 ,即
,即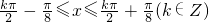 (12分)
(12分)
故函数g(x)的单调增区间为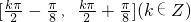 .(13分)
.(13分)
分析:(1)由图象知,周期的四分之一为 ,故周期为T=π,用公式可求出ω的值,又图象过(
,故周期为T=π,用公式可求出ω的值,又图象过( ,0),将其代入方程即可解得∅的值.
,0),将其代入方程即可解得∅的值.
(2)整理出g(x)的表达式,变形为y=asin(ωx+∅)+k的形式,利用其单调性求函数的单调区间.
点评:考查识图的能力与利用 三角恒等变换进行变形的能力,以及形如y=asin(ωx+∅)+k的三角函数求单调区间的方法.
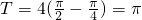 ,
, ,(2分)
,(2分)又由
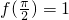 得,sin(π+∅)=1,又f(0)=-1,得sinφ=-1
得,sin(π+∅)=1,又f(0)=-1,得sinφ=-1∵|∅|<π∴
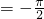 ,(4分)
,(4分)(Ⅱ)由(Ⅰ)知:
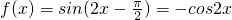 (6分)
(6分)因为
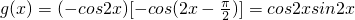 =
=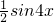 (9分)
(9分)所以,
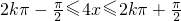 ,即
,即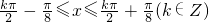 (12分)
(12分)故函数g(x)的单调增区间为
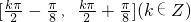 .(13分)
.(13分)分析:(1)由图象知,周期的四分之一为
 ,故周期为T=π,用公式可求出ω的值,又图象过(
,故周期为T=π,用公式可求出ω的值,又图象过( ,0),将其代入方程即可解得∅的值.
,0),将其代入方程即可解得∅的值.(2)整理出g(x)的表达式,变形为y=asin(ωx+∅)+k的形式,利用其单调性求函数的单调区间.
点评:考查识图的能力与利用 三角恒等变换进行变形的能力,以及形如y=asin(ωx+∅)+k的三角函数求单调区间的方法.

练习册系列答案
相关题目
