题目内容
(本小题满分14分)
在一个半径为1的半球材料中截取三个高度均为h的圆柱,其轴截面如图所示,设三个圆柱体积之和为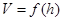 。
。
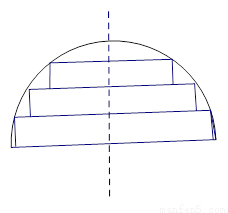
(1) 求f(h)的表达式,并写出h的取值范围是 ;
(2) 求三个圆柱体积之和V的最大值;
【答案】
(1) 的取值范围是
的取值范围是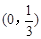 ;⑵三个圆柱体积和
;⑵三个圆柱体积和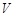 的最大值为
的最大值为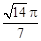 .
.
【解析】本试题是以半球为背景,表示圆柱体的高度的关系式,以及体积的运用,并结合导数来求解最值问题。
(1)利用球的半径和圆柱的高度得到关于r与半径的关系式,从而得到高度的表示。
(2)而圆柱体的体积就是底面积乘以高,那么三个柱体的体积可以借助于第一问中的高度表示出来,再集合导数的思想求解体积的最值。
解:(1)自下而上三个圆柱的底面半径分别为:
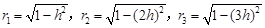 .
………………………………3分
.
………………………………3分
它们的高均为 ,所以体积和
,所以体积和
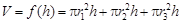
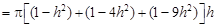
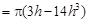 6分
6分
因为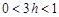 ,所以
,所以 的取值范围是
的取值范围是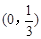 ; ………………………………………7分
; ………………………………………7分
⑵ 由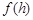
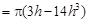 得
得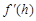
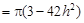
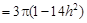 , ………………9分
, ………………9分
又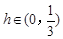 ,所以
,所以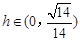 时,
时,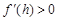 ;
; 时,
时,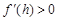 .11分
.11分
所以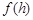 在
在 上为增函数,在
上为增函数,在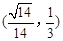 上为减函数,
上为减函数,
所以 时,
时,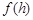 取最大值,
取最大值,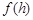 的最大值为
的最大值为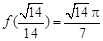 . ………13分
. ………13分
答:三个圆柱体积和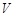 的最大值为
的最大值为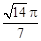 .
…………………………………………14分
.
…………………………………………14分

练习册系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)