题目内容
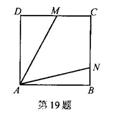
如图所示,四边形ABCD为矩形,点M是BC的中点,CN=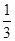 CA,用向量法证明:
CA,用向量法证明:
(1)D、N、M三点共线;(2)若四边形ABCD为正方形,则DN=BN.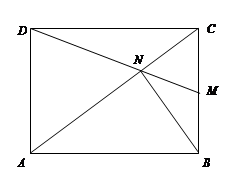

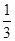 CA,用向量法证明:
CA,用向量法证明:(1)D、N、M三点共线;(2)若四边形ABCD为正方形,则DN=BN.


(1)设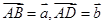
∵
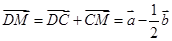 ………3分
………3分
∴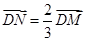 ,且DM与DN有公共点D
,且DM与DN有公共点D
∴D、N、M三点共线
(2)若四边形ABCD为正方形,则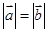 且
且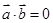
∵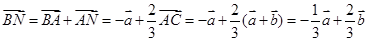
∴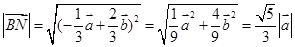
同理可得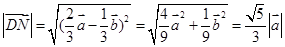 ∴
∴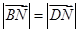 ,即DN=BN
,即DN=BN
备注:利用坐标来运算的相应得分.
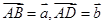
∵

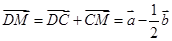 ………3分
………3分∴
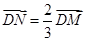 ,且DM与DN有公共点D
,且DM与DN有公共点D∴D、N、M三点共线
(2)若四边形ABCD为正方形,则
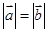 且
且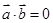
∵
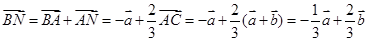
∴
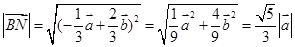
同理可得
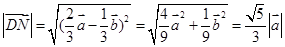 ∴
∴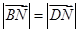 ,即DN=BN
,即DN=BN备注:利用坐标来运算的相应得分.
(1)用向量法证明可以选建立直角坐标系,用向量的坐标运算进行证明三点共线.
(2)线段长度相等就是证明其对应的向量的模相等即可,即证: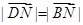 .
.
(2)线段长度相等就是证明其对应的向量的模相等即可,即证:
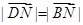 .
.
练习册系列答案
相关题目
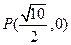 作倾斜角为
作倾斜角为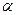 的直线与曲线
的直线与曲线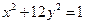 交于点
交于点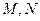 ,
,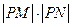 的值及相应的
的值及相应的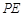 切⊙
切⊙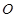 于点E,割线PBA交⊙
于点E,割线PBA交⊙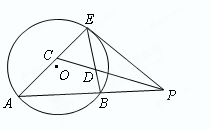
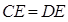 ;
;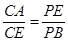 .
.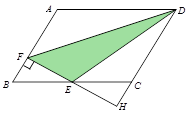
 中,
中,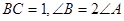 ,则
,则 的取值范围是( )
的取值范围是( )



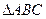 中,
中,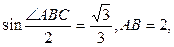
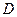 在线
在线 段
段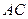 上,且
上,且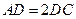 ,
,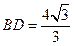
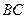 的长;
的长;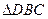 的面积.
的面积.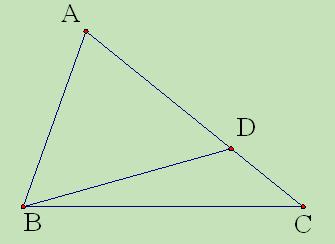
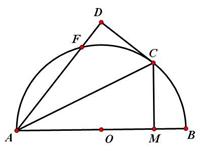
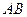 是⊙
是⊙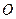 的直径,
的直径,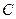 、
、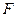 是⊙
是⊙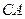 是
是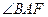 的角平分线,过点
的角平分线,过点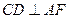 ,交
,交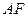 的延长线于
的延长线于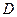 点,
点,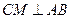 ,垂足为点
,垂足为点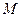 ,
,
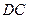 是⊙
是⊙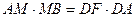
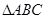 中,
中,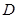 为
为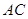 边上的中点,
边上的中点,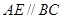 ,
,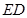 交
交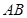 于点
于点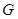 ,交
,交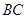 延长线于点
延长线于点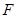 ,若
,若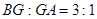 ,
,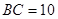 ,则
,则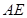 的长为 .
的长为 .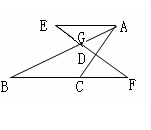
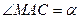 ,那么
,那么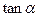 的值等于 。
的值等于 。