题目内容
如图,在□ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H,则△DEF的面积是 .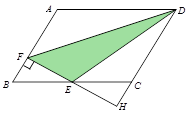

2

解:∵四边形ABCD是平行四边形,
∴AD=BC=4,AB∥CD,AB=CD=3,
∵E为BC中点,
∴BE=CE=2,
∵∠B=60°,EF⊥AB,
∴∠FEB=30°,
∴BF=1,
由勾股定理得:EF=" 3" ,
∵AB∥CD,
∴△BFE∽△CHE,
∴EF :EH ="BE" :CE =BF: CH ="2" :2 =1,
∴EF="EH=" 3 ,CH=BF=1,
∵S△DHF= DH•FH=
DH•FH= ×(1+3)×2
×(1+3)×2 =4
=4 ,
,
∴S△DEF= S△DHF=2
S△DHF=2 ,
,
故答案为:2
∴AD=BC=4,AB∥CD,AB=CD=3,
∵E为BC中点,
∴BE=CE=2,
∵∠B=60°,EF⊥AB,
∴∠FEB=30°,
∴BF=1,
由勾股定理得:EF=" 3" ,
∵AB∥CD,
∴△BFE∽△CHE,
∴EF :EH ="BE" :CE =BF: CH ="2" :2 =1,
∴EF="EH=" 3 ,CH=BF=1,
∵S△DHF=
 DH•FH=
DH•FH= ×(1+3)×2
×(1+3)×2 =4
=4 ,
,∴S△DEF=
 S△DHF=2
S△DHF=2 ,
,故答案为:2


练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目





 CA,用向量法证明:
CA,用向量法证明: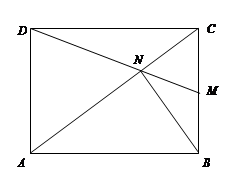

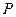 为
为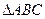 内一点,且
内一点,且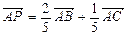 ,则
,则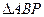 的面积与
的面积与 面积之比等于( ).
面积之比等于( ).



 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心, 为半径的圆弧与以
为半径的圆弧与以 为直径的半⊙O交于点
为直径的半⊙O交于点 ,延长
,延长 交
交 于
于 .
. 的长.
的长.