题目内容
9．设实数x，y满足$\left\{\begin{array}{l}x≤y\\ y≤6-2x\\ x≥1\end{array}\right.$，则目标函数m=-2x+y的最小值为-2．分析 作出不等式对应的平面区域，利用z的几何意义分行求解即可
解答 解：实数x，y满足$\left\{\begin{array}{l}x≤y\\ y≤6-2x\\ x≥1\end{array}\right.$的平面区域如图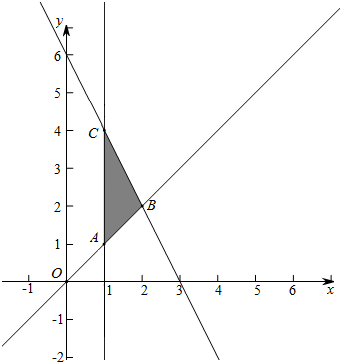
目标函数m=-2x+y经过B时最小，解$\left\{\begin{array}{l}{y=x}\\{y=6-2x}\end{array}\right.$得B（2，2），所以最小值为-2×2+2=-2；
故答案为：-2．
点评 本题主要考查线性规划的基本应用，利用z的几何意义是解决线性规划问题的关键，注意利用数形结合来解决．
练习册系列答案
相关题目
一个四棱锥的正视图，侧视图（单位：cm）如图所示，
20．某企业生产A，B，C三种产品，每种产品有M和N两个型号．经统计三月下旬该企业的产量如下表（单位：件）．用分层抽样的方法从这月下旬生产的三种产品中抽取50件调查，其中抽到A种产品10件．
（1）求x的值；
（2）用分层抽样方法在C产品中抽取一个容量为5的样本，将该样本看作一个总体，从中任取两件，求至少有一件是M型号的概率；
（3）用随机抽样的方法从C产品中抽取8件产品做用户满意度调查，经统计它们的得分如下：9.4，8.6，9.2，9.6，8.7，9.3，9.0，8.2．把8件产品的得分看作一个样本，从中任取一个数，求该数与样本平均数之差的绝对值超过0.5的概率．
| A | B | C | |
| M | 200 | 300 | 240 |
| N | 200 | 700 | x |
（2）用分层抽样方法在C产品中抽取一个容量为5的样本，将该样本看作一个总体，从中任取两件，求至少有一件是M型号的概率；
（3）用随机抽样的方法从C产品中抽取8件产品做用户满意度调查，经统计它们的得分如下：9.4，8.6，9.2，9.6，8.7，9.3，9.0，8.2．把8件产品的得分看作一个样本，从中任取一个数，求该数与样本平均数之差的绝对值超过0.5的概率．
14．已知全集U={a，b，c，d}，集合M={a，b}，N={b，c}，则∁U（M∪N）=（ ）
| A． | {a，c，d} | B． | {a，b，c} | C． | {c} | D． | {d} |