题目内容
16.已知sin(α-$\frac{π}{4}$)=$\frac{\sqrt{3}}{2}$,则sin($\frac{5π}{4}$-α)的值为$\frac{\sqrt{3}}{2}$.分析 由条件利用诱导公式化简所给的三角函数式,可得结果.
解答 解:∵sin(α-$\frac{π}{4}$)=$\frac{\sqrt{3}}{2}$,则sin($\frac{5π}{4}$-α)=sin[π+($\frac{π}{4}$-α)]=-sin($\frac{π}{4}$-α)=son(α-$\frac{π}{4}$)=$\frac{\sqrt{3}}{2}$,
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题主要考查利用诱导公式进行化简求值,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
6.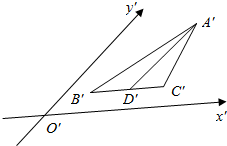 如图所示的水平放置的三角形的直观图中,D′是△A′B′C′中B′C′边的中点,那么A′B′,A′D′,A′C′三条线段对应原图形中线段AB,AD,AC中( )
如图所示的水平放置的三角形的直观图中,D′是△A′B′C′中B′C′边的中点,那么A′B′,A′D′,A′C′三条线段对应原图形中线段AB,AD,AC中( )
 如图所示的水平放置的三角形的直观图中,D′是△A′B′C′中B′C′边的中点,那么A′B′,A′D′,A′C′三条线段对应原图形中线段AB,AD,AC中( )
如图所示的水平放置的三角形的直观图中,D′是△A′B′C′中B′C′边的中点,那么A′B′,A′D′,A′C′三条线段对应原图形中线段AB,AD,AC中( )| A. | 最长的是AB,最短的是AC | B. | 最长的是AC,最短的是AB | ||
| C. | 最长的是AB,最短的是AD | D. | 最长的是AD,最短的是AC |
4.非零向量 $\overrightarrow{a}$,$\overrightarrow{b}$夹角为120°,且|$\overrightarrow{a}$-$\overrightarrow{b}$|=2,则|$\overrightarrow{a}$+$\overrightarrow{b}$|的取值范围为( )
| A. | [1,$\sqrt{3}$] | B. | [2,$\frac{4\sqrt{3}}{3}$] | C. | [$\frac{2\sqrt{3}}{3}$,4) | D. | [1,2] |