题目内容
13.设函数f(x)=4x3+ax+2,曲线y=f(x)在点P(0,2)处切线的斜率为-12,求:(1)a的值;
(2)函数f(x)在区间[-3,2]的最大值与最小值.
分析 (1)求得f(x)的导数,求得切线的斜率,由条件可得a=-12;
(2)求得f(x)的解析式和导数,令导数为0,可得极值点,求得极值,再由端点的函数值,即可得到最值.
解答 解:(1)函数f(x)=4x3+ax+2的导数为f′(x)=12x2+a,
在点P(0,2)处切线的斜率为-12,即有a=-12;
(2)f(x)=4x3+12x+2的导数为
f′(x)=12x2-12=12(x-1)(x+1),
由f′(x)=0解得x=±1∈[-3,2],
由f(-1)=-14,f(1)=18,f(-3)=-142,f(2)=58,
可得最小值为f(-3)=-142,最大值为f(2)=58.
点评 本题考查导数的运用:求切线的斜率和单调区间、最值,考查运算能力,属于中档题.

练习册系列答案
相关题目
5.如图所示,已知|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=1,AB的中点是C,则$\overrightarrow{OC}$的坐标是( )
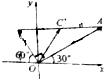

| A. | ($\frac{\sqrt{3}}{4}$-$\frac{1}{4}$,$\frac{1}{2}$+$\frac{\sqrt{3}}{4}$) | B. | ($\frac{\sqrt{3}}{2}$-$\frac{1}{2}$,$\frac{1}{2}$-$\frac{\sqrt{3}}{4}$) | C. | ($\frac{\sqrt{3}}{2}$-$\frac{1}{4}$,$\frac{1}{2}$+$\frac{\sqrt{3}}{4}$) | D. | ($\frac{\sqrt{3}}{2}$-$\frac{1}{4}$,$\frac{\sqrt{3}}{4}$-$\frac{1}{2}$) |