题目内容
设函数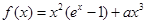
(1)当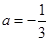 时,求
时,求 的单调区间;
的单调区间;
(2)若当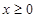 时
时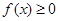 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(1)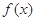 的单调递增区间为
的单调递增区间为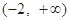 ,
,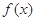 的单调递减区间为
的单调递减区间为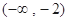 ;
;
(2)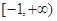
解析试题分析:(1)将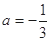 代入,求导即可 (2)注意
代入,求导即可 (2)注意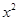 恒大于等于0,故只需
恒大于等于0,故只需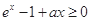 对任意
对任意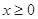 恒成立即可 接下来就利用导数研究函数
恒成立即可 接下来就利用导数研究函数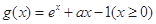
试题解析:(1)当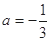 时,
时,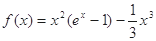
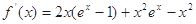
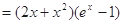
令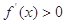 ,得
,得 或
或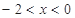 ;令
;令 ,得
,得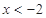
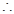
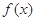 的单调递增区间为
的单调递增区间为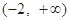
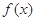 的单调递减区间为
的单调递减区间为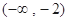 6分
6分
(2)因为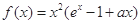 对任意
对任意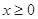 ,设
,设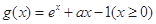
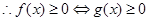
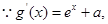
当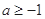 时,
时,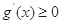 对
对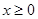 恒成立,
恒成立,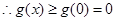 符合题意 9分
符合题意 9分
当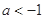 时,由
时,由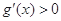 得
得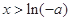 ;由
;由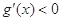 得
得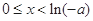 ;
;
所以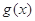 在
在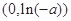 上是减函数,在
上是减函数,在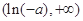 上是增函数
上是增函数
又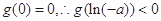 ,故不符合题意 12分
,故不符合题意 12分
综上所述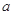 的取值范围是
的取值范围是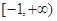 13分
13分
考点:1、导数的应用;2、不等关系

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
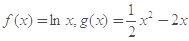 .
.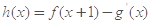 (其中
(其中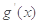 是
是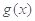 的导函数),求
的导函数),求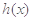 的最大值;
的最大值;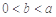 时,有
时,有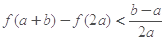 ;
;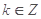 ,当
,当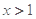 时,不等式
时,不等式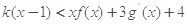 恒成立,求
恒成立,求 的最大值.
的最大值.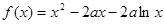 (
(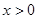 ,
,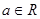 ),
),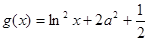 .
.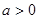 时,对于任意不相等的两个正实数
时,对于任意不相等的两个正实数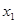 、
、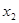 ,均有
,均有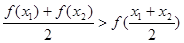 成立;
成立; ,若
,若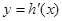 在
在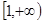 上单调递增,求实数
上单调递增,求实数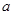 的取值范围;
的取值范围;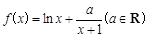 .
.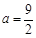 时,如果函数
时,如果函数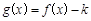 仅有一个零点,求实数
仅有一个零点,求实数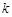 的取值范围;
的取值范围;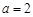 时,试比较
时,试比较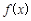 与1的大小;
与1的大小;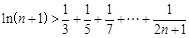
 排水管,在路南侧沿直线
排水管,在路南侧沿直线 排水管(假设水管与公路的南,北侧在一条直线上且水管的大小看作为一条直线),现要在矩形区域ABCD内沿直线EF将
排水管(假设水管与公路的南,北侧在一条直线上且水管的大小看作为一条直线),现要在矩形区域ABCD内沿直线EF将 m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成角为
m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成角为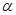 .矩形区域内的排管费用为W.
.矩形区域内的排管费用为W.
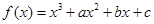 在
在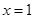 与
与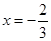 时,都取得极值.
时,都取得极值.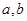 的值;
的值;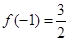 ,求
,求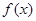 的单调区间和极值;
的单调区间和极值; 都有
都有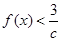 恒成立,求
恒成立,求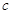 的取值范围.
的取值范围.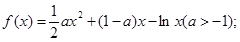
 的单调区间;
的单调区间; 使
使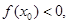 求实数a的范围.
求实数a的范围.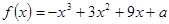 .
. 的单调递减区间;
的单调递减区间;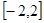 上的最大值为
上的最大值为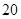 ,求它在该区间上的最小值.
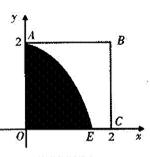
,求它在该区间上的最小值.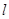 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数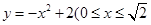 的图象,且点M到边OA距离为
的图象,且点M到边OA距离为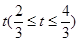 .
.
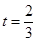 时,求直路
时,求直路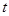 为何值时,地块OABC在直路
为何值时,地块OABC在直路