题目内容
如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线 排水管,在路南侧沿直线
排水管,在路南侧沿直线 排水管(假设水管与公路的南,北侧在一条直线上且水管的大小看作为一条直线),现要在矩形区域ABCD内沿直线EF将
排水管(假设水管与公路的南,北侧在一条直线上且水管的大小看作为一条直线),现要在矩形区域ABCD内沿直线EF将 与
与 接通.已知AB = 60m,BC = 60
接通.已知AB = 60m,BC = 60 m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成角为
m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成角为 .矩形区域内的排管费用为W.
.矩形区域内的排管费用为W.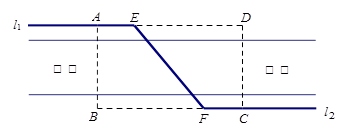
(1)求W关于 的函数关系式;
的函数关系式;
(2)求W的最小值及相应的角 .
.
(1) ;(2)
;(2)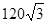 ,
, .
.
解析试题分析:(1)过E作 ,垂足为
,垂足为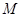 ,然后将
,然后将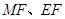 用
用 ,再根据题意列出W关于
,再根据题意列出W关于 的函数关系式,化简即得
的函数关系式,化简即得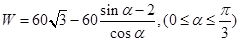 ;(2)设
;(2)设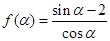 ,
,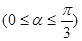 ,再对其求导,通过导函数确定在
,再对其求导,通过导函数确定在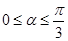 的单调性,从而得到该函数的最大值以及取得最大值时相应的角
的单调性,从而得到该函数的最大值以及取得最大值时相应的角 ,代入
,代入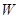 中,即得到W的最小值.
中,即得到W的最小值.
试题解析:(1)如图,过E作 ,垂足为
,垂足为 ,由题意得
,由题意得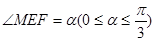 ,
,
故有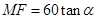 ,
, ,
, 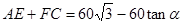 ,
,
所以W= .
.
即  . 6分
. 6分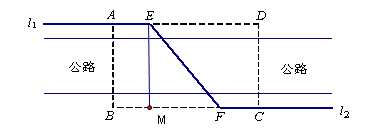
(2)设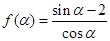 ,
,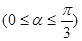
则 .
.
令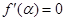 得
得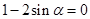 ,即
,即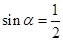 ,得
,得 .
.
列表
所以当


+ 0 - 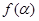
单调递增 极大值 单调递减  时有
时有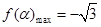 ,此时有.
,此时有.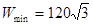
答:排管的最小费用为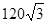 万元,相应的角
万元,相应的角 . 13分
. 13分
考点:1.三角函数;2.用导数研究函数的单调性;3.利用单调性求最值.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
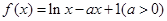 。
。 的零点个数;
的零点个数;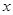 轴交于
轴交于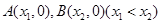 两点,
两点,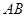 中点为
中点为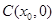 ,设函数
,设函数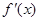 , 求证:
, 求证: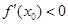 。
。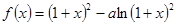 在
在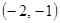 上是增函数,
上是增函数,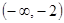 上是减函数.
上是减函数. 的解析式;
的解析式; 时,
时,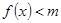 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围; 在区间
在区间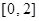 上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由. 的导函数是
的导函数是 ,
,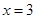 处取得极值,且
处取得极值,且 .
. 上的最大值为
上的最大值为 ,若对任意的
,若对任意的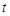
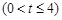 总有
总有 成立,求
成立,求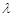 的取值范围;
的取值范围; 是曲线
是曲线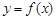 上的任意一点.当
上的任意一点.当 时,求直线OM斜率的最小值,据此判断
时,求直线OM斜率的最小值,据此判断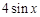 的大小关系,并说明理由.
的大小关系,并说明理由.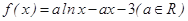 .
. ,求函数
,求函数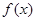 的单调区间;
的单调区间;
 的图象在点
的图象在点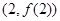 处的切线的倾斜角为
处的切线的倾斜角为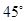 ,对于任意的
,对于任意的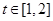 ,函数
,函数 是
是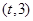 上总不是单调函数,求
上总不是单调函数,求 的取值范围。
的取值范围。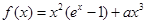
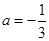 时,求
时,求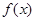 的单调区间;
的单调区间; 时
时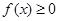 恒成立,求实数
恒成立,求实数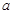 的取值范围。
的取值范围。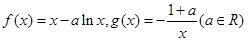 .
.  时,求曲线
时,求曲线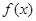 在
在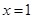 处的切线方程;
处的切线方程;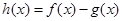 ,求函数
,求函数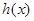 的单调区间;
的单调区间; 上存在一点
上存在一点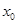 ,使得
,使得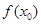 <
< 成立,求
成立,求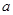 的取值范围.
的取值范围.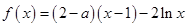 ,
, (
( ,
, 为自然对数的底数).
为自然对数的底数). 时,求
时,求 的单调区间;
的单调区间; ,
, 恒成立,求
恒成立,求 的最小值;
的最小值; ,在
,在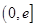 上总存在两个不同的
上总存在两个不同的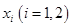 ,使得
,使得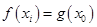 成立,求
成立,求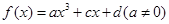 是R上的奇函数,当
是R上的奇函数,当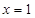 时
时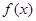 取得极值
取得极值 .
.
 不等式
不等式 恒成立.
恒成立.