题目内容
已知函数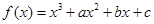 在
在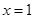 与
与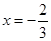 时,都取得极值.
时,都取得极值.
(1)求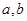 的值;
的值;
(2)若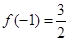 ,求
,求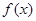 的单调区间和极值;
的单调区间和极值;
(3)若对 都有
都有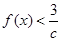 恒成立,求
恒成立,求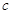 的取值范围.
的取值范围.
(1)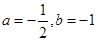 ;(2)f (x)的递增区间为(-∞,-
;(2)f (x)的递增区间为(-∞,-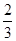 ),及(1,+∞),递减区间为(-
),及(1,+∞),递减区间为(-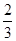 ,1),当x=-
,1),当x=-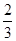 时,f (x)有极大值,f (-
时,f (x)有极大值,f (-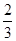 )=
)=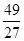 ;当x=1时,f (x)有极小值,f (1)=-
;当x=1时,f (x)有极小值,f (1)=- ;(3)
;(3)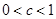 或
或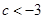 .
.
解析试题分析:(1)函数的极值点是使导数等于0的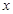 的值,因此本题中一定有
的值,因此本题中一定有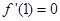 和
和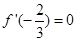 ,由此可解出
,由此可解出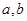 的值;(2)再由
的值;(2)再由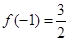 可求出
可求出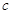 ,而求单调区间,很显然是解不等式
,而求单调区间,很显然是解不等式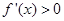 (得增区间)或
(得增区间)或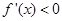 (得减区间),然后可得相应的极大值和极小值;(3)
(得减区间),然后可得相应的极大值和极小值;(3) 不等式
不等式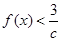 恒成立,实际上就是当
恒成立,实际上就是当 时
时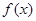 的最大值小于
的最大值小于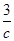 ,因此问题转化为先求
,因此问题转化为先求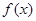 在
在 上的最大值
上的最大值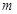 ,然后再解不等式
,然后再解不等式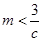 即可.
即可.
试题解析:(1)f ′(x)=3x2+2a x+b=0.
由题设,x=1,x=-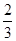 为f ′(x)=0的解.
为f ′(x)=0的解.
-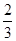 a=1-
a=1-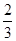 ,
,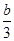 =1×(-
=1×(-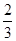 ).∴a=-
).∴a=- ,b=-2 3分
,b=-2 3分
经检验得:这时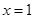 与
与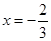 都是极值点. …4分
都是极值点. …4分
(2)f (x)=x3- x2-2 x+c,由f (-1)=-1-
x2-2 x+c,由f (-1)=-1- +2+c=
+2+c=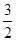 ,c=1.
,c=1.
∴f (x)=x3- x2-2 x+1.
x2-2 x+1.
∴f(x)的递增区间为(-∞,-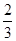 ),及(1,+∞),递减区间为(-
),及(1,+∞),递减区间为(-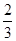 ,1).
,1).
当x=-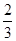 时,f (x)有极大值,f (-
时,f (x)有极大值,f (-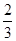 )=
)=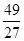 ;
;
当x=1时,f (x)有极小值,f (1)=- …8分
…8分
(3)由(1)得,f′(x)=(x-1)(3x+2),f (x)=x3- x2-2 x+c,
x2-2 x+c,
f (x)在[-1,-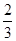
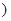 及(1,2]上递增,在(-
及(1,2]上递增,在(-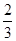 ,1)递减.
,1)递减.
而f (-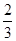 )=-
)=-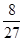 -
-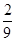 +
+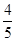 +c=c+
+c=c+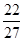 .f (2)=8-2-4+c=c+2.
.f (2)=8-2-4+c=c+2.
∴ f (x)在[-1,2]上的最大值为c+2.∴ 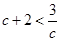 ,∴
,∴ 
∴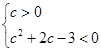 或
或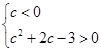 ∴
∴ 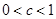 或
或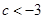 12分
12分
考点:(1)导数与极值;(2)导数与单调区间;(3)不等式恒成立问题.

 ,若
,若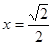 时,
时,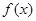 有极小值
有极小值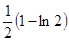 ,
,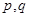 的取值;
的取值;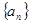 中,
中,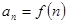 ,求证:数列
,求证:数列 项和
项和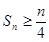 ;
;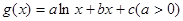 ,若
,若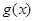 有极值且极值为
有极值且极值为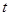 ,则
,则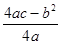 是否具有确定的大小关系?证明你的结论.
是否具有确定的大小关系?证明你的结论.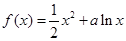 .
.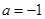 ,求函数
,求函数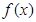 的极值,并指出是极大值还是极小值;
的极值,并指出是极大值还是极小值;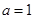 ,求证:在区间
,求证:在区间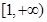 上,函数
上,函数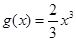 的图像的下方.
的图像的下方.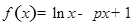 .
.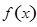 的极值点;
的极值点;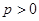 时,若对任意的
时,若对任意的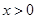 ,恒有
,恒有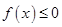 ,求
,求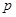 的取值范围;
的取值范围;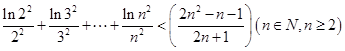 .
.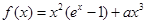
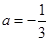 时,求
时,求 的单调区间;
的单调区间;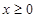 时
时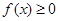 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 元,则销售量
元,则销售量 (单位:件)与零售价
(单位:件)与零售价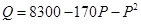 ,问该商品零售价定为多少元时毛利润
,问该商品零售价定为多少元时毛利润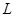 最大,并求出最大毛利润.(毛利润
最大,并求出最大毛利润.(毛利润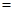 销售收入
销售收入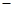 进货支出)
进货支出)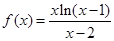 .
.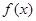 的单调性;
的单调性;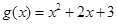 ,证明:对任意
,证明:对任意 ,总存在
,总存在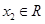 ,使得
,使得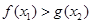 .
.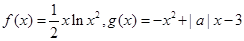 。
。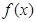 在
在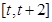
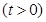 上的最小值;
上的最小值;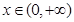 ,
,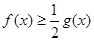 恒成立,求实数
恒成立,求实数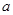 的取值范围.
的取值范围. ,
, 为自然对数的底,
为自然对数的底, 的最值;
的最值;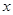 方程
方程 有两个不同解,求
有两个不同解,求 的范围.
的范围.