题目内容
(本小题12分)某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2
表1:
| 生产能力分组 | 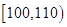 | 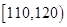 | 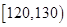 | 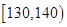 | 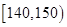 |
| 人数 | 4 | 8 |  | 5 | 3 |
| 生产能力分组 | 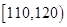 | 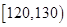 | 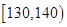 | 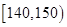 |
| 人数 | 6 | y | 36 | 18 |
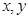 ,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
(2)分别估计
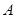 类工人和
类工人和 类工人生产能力的众数、中位数和平均数。(精确到0.1)
类工人生产能力的众数、中位数和平均数。(精确到0.1)
解:(1)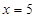 ;
;  。频率分布直方图如下:
。频率分布直方图如下: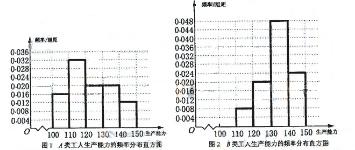
从直方图可以判断: 类工人中个体间的差异程度更小。
类工人中个体间的差异程度更小。
(2)A类工人生产能力的平均数、B类工人生产能力的平均数的估计值分别为123,133.8。
解析试题分析:(1)根据随机抽样中各个个体被抽到的可能性均相等,可以得出甲、乙两工人分别被抽到的概率,再根据独立事件概率的计算公式求得结果;
(2)①利用分层抽样的思想确定出A类工人和B类工人分别被抽查到的人数,然后根据统计表格利用方程确定出x,y的值,完成频率分布直方图,通过频率分布直方图判断出A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小;
②利用频率分布直方图各组小长方形上端的中点横坐标作为该组的生产能力估计值,各组的频率值作为近似的概率值利用均值的计算公式估算出他们的生产能力平均数.
解:(1)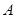 类工人中和
类工人中和 类工人中分别抽查25名和75名。由
类工人中分别抽查25名和75名。由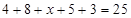 ,得
,得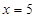 ;
;  ,得
,得 。
。
频率分布直方图如下:
从直方图可以判断: 类工人中个体间的差异程度更小。
类工人中个体间的差异程度更小。
(2)A类工人生产能力的众数、 B类工人生产能力的众数的估计值为115,135;
A类工人生产能力的中位数、B类工人生产能力的中位数的估计值为121,134.6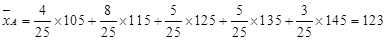
 ,
,
A类工人生产能力的平均数、B类工人生产能力的平均数的估计值分别为123,133.8。
考点:本试题主要考查了统计的基本知识,考查用样本估计总体的思想,考查随机抽样的基本思想和方法,分层抽样的思想、相互独立事件同时发生的概率的计算方法,考查频率分布直方图的绘画、学生的画图、识图能力,数据平均值的计算方法.
点评:易错点就是对于均值的求解不知道如何结合图像来求解。解决该试题的关键是理解分层抽样法以及频率分布直方图和数据的平均值的的求解公式。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案(本题满分12分)
某车间为了规定工时定额,需要确定加共某零件所花费的时间,为此作了四次实验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(2)试预测加工10个零件需要多少时间?
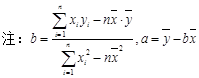
(本小题满分12分)一个容量为M的样本数据,其频率分布表如下.
(Ⅰ)表中a= ,b = ;
(Ⅱ)画出频率分布直方图;
(Ⅲ)用频率分布直方图,求出总体的众数及平均数的估计值.
频率分布表
| 分组 | 频数 | 频率 | 频率/组距 |
| (10,20] | 2 | 0.10 | 0.010 |
| (20,30] | 3 | 0.15 | 0.015 |
| (30,40] | 4 | 0.20 | 0.020 |
| (40,50] | a | b | 0.025 |
| (50,60] | 4 | 0.20 | 0.020 |
| (60, 70] | 2 | 0.10 | 0.010 |
频率分布直方图
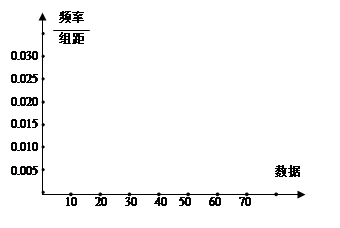
对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图,由茎叶图判断哪位选手的成绩较稳定?
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、标准差,并判断选谁参加比赛更合适.
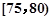 ,第2组
,第2组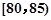 ,第3组
,第3组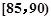 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.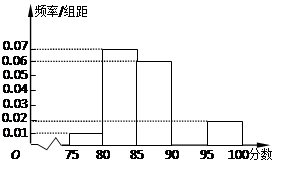
 男 女
男 女 15 7 7 8 9 9 9
15 7 7 8 9 9 9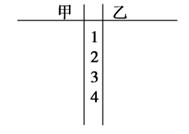
 ,将这10株树苗的高度依次输入如图程序框图进行运算,问输出的S大小为多少?并说明S的统计学意义.
,将这10株树苗的高度依次输入如图程序框图进行运算,问输出的S大小为多少?并说明S的统计学意义.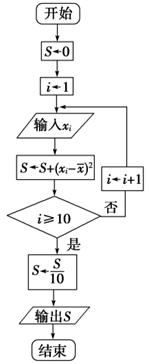
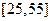 岁的人群随机抽取
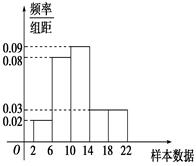
岁的人群随机抽取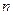 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图: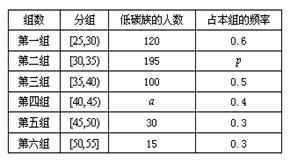
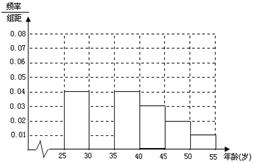
 、
、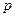 的值;
的值;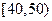 的“低碳族”中采用分层抽样法抽取
的“低碳族”中采用分层抽样法抽取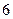 人参加户外低碳体验活动,其中选取
人参加户外低碳体验活动,其中选取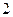 人作为领队,求选取的
人作为领队,求选取的 岁的概率。
岁的概率。