题目内容
【题目】某企业经过短短几年的发展,员工近百人.不知何因,人员虽然多了,但员工的实际工作效率还不如从前.![]() 年
年![]() 月初,企业领导按员工年龄从企业抽选
月初,企业领导按员工年龄从企业抽选![]() 位员工交流,并将被抽取的员工按年龄(单位:岁)分为四组:第一组
位员工交流,并将被抽取的员工按年龄(单位:岁)分为四组:第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组
,第四组![]() ,且得到如下频率分布直方图:
,且得到如下频率分布直方图:

(1)求实数![]() 的值;
的值;
(2)若用简单随机抽样方法从第二组、第三组中再随机抽取![]() 人作进一步交流,求“被抽取得
人作进一步交流,求“被抽取得![]() 人均来自第二组”的概率.
人均来自第二组”的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用频率分布直方图所有矩形的面积和为![]() 可求出实数
可求出实数![]() 的值;
的值;
(2)可知第二组的人数为![]() 人,第三组的人数为
人,第三组的人数为![]() 人,利用组合计数原理计算出抽取
人,利用组合计数原理计算出抽取![]() 人的方法种数,以及抽取的
人的方法种数,以及抽取的![]() 人均来自第二组的方法种数,利用古典概型的概率公式可计算出所求事件的概率.
人均来自第二组的方法种数,利用古典概型的概率公式可计算出所求事件的概率.
(1)据题意得![]() ,解得
,解得![]() ;
;
(2)据(1)求解知![]() ,
,
![]() 第二组中人数
第二组中人数![]() (人)又第三组人数
(人)又第三组人数![]() (人),
(人),
![]() 用简单随机抽样方法从第二组、第三组中抽取
用简单随机抽样方法从第二组、第三组中抽取![]() 人的方法数
人的方法数![]() (种)
(种)
其中![]() 人均来自第二组的方法数
人均来自第二组的方法数![]() (种),因此,所求的概率
(种),因此,所求的概率![]() .
.

 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案【题目】为了调查某社区居民每天参加健身的时间,某机构在该社区随机采访男性、女性各50名,其中每人每天的健身时间不少于1小时称为“健身族”,否则称其为"非健身族”,调查结果如下:
健身族 | 非健身族 | 合计 | |
男性 | 40 | 10 | 50 |
女性 | 30 | 20 | 50 |
合计 | 70 | 30 | 100 |
(1)若居民每人每天的平均健身时间不低于70分钟,则称该社区为“健身社区”. 已知被随机采访的男性健身族,男性非健身族,女性健身族,女性非健身族每人每天的平均健分时间分別是1.2小时,0.8小时,1.5小时,0.7小时,试估计该社区可否称为“健身社区”?
(2)根据以上数据,能否在犯错误的概率不超过5%的情况下认为“健身族”与“性别”有关?
参考公式: 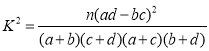 ,其中
,其中![]() .
.
参考数据:
| 0. 50 | 0. 40 | 0. 25 | 0. 05 | 0. 025 | 0. 010 |
| 0. 455 | 0. 708 | 1. 321 | 3. 840 | 5. 024 | 6. 635 |
【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用列联表,由计算可得![]() ,参照下表:
,参照下表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是( )
A.有![]() 以上的把握认为“爱好该项运动与性别无关”
以上的把握认为“爱好该项运动与性别无关”
B.有![]() 以上的把握认为“爱好该项运动与性别有关”
以上的把握认为“爱好该项运动与性别有关”
C.在犯错误的概率不超过![]() 的前提下,认为“爱好该项运动与性别有关”
的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过![]() 的前提下,认为“爱好该项运动与性别无关”
的前提下,认为“爱好该项运动与性别无关”


