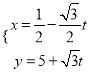题目内容
【题目】椭圆C的中心在坐标原点，焦点在x轴上，该椭圆经过点 
且离心率为 
．
（1）求椭圆C的标准方程；
（2）若直线l：y=kx+m与椭圆C相交A，B两点（A，B不是左右顶点），且以AB为直径的圆过椭圆C的右顶点，求证：直线l过定点，并求出该定点的坐标．
【答案】
（1）解：椭圆的标准方程为 
（2）解：设A（x1，y1），B（x2，y2），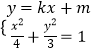 
得：（3+4k2）x2+8kmx+4（m2﹣3）=0，
∵△＞0，∴3+4k2﹣m2＞0，
∴ 
∵以AB为直径的圆过椭圆C的右顶点，∴kADkBD=﹣1，
∴y1y2+x1x2﹣2（x1+x2）+4=0，∴7m2+16mk+4k2=0，
∴m1=﹣2k， 
k，且均满足3+4k2﹣m2＞0，
当m1=﹣2k时，l的方程为y=k（x﹣2），则直线过定点（2，0）与已知矛盾
当 
时，l的方程为 
，则直线过定点 
∴直线l过定点，定点坐标为
【解析】（1）根据椭圆的方程和简单几何性质，使用待定系数法即可；（2）要证明直线系y=kx+m过定点，就要找到其中的参数k，m之间的关系，把双参数化为但参数问题解决，这只要根据直线l：y=kx+m与椭圆C相交A，B两点（A，B不是左右顶点），且以AB为直径的圆过椭圆C的右顶点即可，这个问题等价于椭圆的右顶点与A，B的张角是直角．
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
．
【题目】某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温（单位： 
）有关．如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间
，需求量为300瓶；如果最高气温低于20，需求量为200瓶，为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：
最高气温 |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率．
（1）求六月份这种酸奶一天的需求量
（单位：瓶）的分布列；
（2）设六月份一天销售这种酸奶的利润为
（单位：元）．当六月份这种酸奶一天的进货量（单位：瓶）为多少时， 
的数学期望达到最大值？
