题目内容
【题目】平面内动点P(x,y)与两定点A(-2, 0), B(2,0)连线的斜率之积等于![]() ,若点P的轨迹为曲线E,过点Q
,若点P的轨迹为曲线E,过点Q![]() 作斜率不为零的直线
作斜率不为零的直线![]() 交曲线E于点
交曲线E于点![]() .
.
(I)求曲线E的方程;
(II)求证: ![]() ;
;
(III)求![]() 面积的最大值.
面积的最大值.
【答案】(1) ![]()
![]() (2)
(2) ![]()
![]() 的面积最大为
的面积最大为![]()
【解析】试题分析:(1)由条件斜率之积等于![]() ,化简即可求出曲线方程;
,化简即可求出曲线方程;
(2)设![]() 方程为
方程为![]() ,与椭圆联立,利用向量的数量积为零,即可证明;
,与椭圆联立,利用向量的数量积为零,即可证明;
(3)利用分割的方法求出三角形面积,利用二次函数求最值得到三角形面积的最值.
试题解析:
(I)设动点P坐标为![]() ,当
,当![]() 时,由条件得:
时,由条件得:
![]() ,化简得
,化简得![]() ,
,
故曲线E的方程为![]()
![]() .
.
(II)![]() 斜率不为0,所以可设
斜率不为0,所以可设![]() 方程为
方程为![]() ,与椭圆联立得:
,与椭圆联立得: ![]() 设
设![]() , 所以
, 所以![]() ,.
,.
![]()
=![]()
所以![]()
![]()
![]()
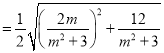
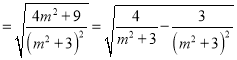
=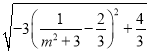 ,这里
,这里![]()
当![]()
![]() 的面积最大为
的面积最大为![]() .
.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目