题目内容
12.已知函数f(x)=ln(x+1)+ax2-2x+1;(1)求函数曲线在x=0处的切线方程;
(2)函数f(x)不单调,求参数a的范围;
(3)曲线C:y=f(x)与(1)中的切线只有一个公共点,求实数a的取值范围.
分析 (1)根据导数的几何意义求出函数f(x)在x=0处的导数,求出切线的斜率,再用点斜式写出切线方程,化成一般式即可;
(2)求出函数f(x)的定义域,化简f′(x)的表达式,将条件转化为:f′(0)=0有解,对讨论a与0的关系,根据导数与函数的单调性,以及二次函数的图象与性质,分别列出不等式组,求出a的取值范围;
(2)将条件转化为:方程ax2-2x+1+ln(x+1)=-x+1即ax2-x+ln(x+1)=0有且只有一个实数解.令h(x)=ax2-x+ln(x+1),求出h'(x),然后讨论a与0、$\frac{1}{2}$的大小,利用导数研究函数的单调性,利用函数的单调性与特殊的函数值,分别求出满足使方程h(x)=0有一解x=0的a的取值范围即可.
解答 解:(1)由题意得,$f′(x)=\frac{1}{x+1}+2ax-2$,且f(0)=1,
所以曲线在x=0处的切线斜率k=f′(0)=-1,
则曲线在x=0处的切线方程是y-1=-x,即x+y-1=0;
(2)函数f(x)的定义域是(-1,+∞),且$f′(x)=\frac{1}{x+1}+2ax-2$=$\frac{2a{x}^{2}+(2a-2)x-1}{x+1}$,
因为函数f(x)不单调,所以f′(0)=0有解,
即2ax2+(2a-2)x-1=0在(-1,+∞)上有解,
①当a=0时,方程为-2x-1=0,得x=$-\frac{1}{2}$>-1,成立,
②当a≠0时,函数y=2ax2+(2a-2)x-1的对称轴x=$-1+\frac{1}{a}$,
所以$\left\{\begin{array}{l}{a>0}\\{△=4(a-1)^{2}+8a>0}\end{array}\right.$或$\left\{\begin{array}{l}{a<0}\\{f(-1)=2a-(2a-2)-1>0}\end{array}\right.$,
解得a>0或a<0,
综上可得,参数a的范围是R;
(3)由(1)得,切线与曲线y=f(x)有且只有一个公共点等价于
方程ax2-2x+1+ln(x+1)=-x+1即ax2-x+ln(x+1)=0有且只有一个实数解.
令h(x)=ax2-x+ln(x+1),x∈(-1,+∞),
∵h(0)=0,∴方程h(x)=0有一解x=0,
则h′(x)=2ax-1+$\frac{1}{x+1}$=$\frac{2a{x}^{2}+(2a-1)x}{x+1}$=$\frac{x(2ax+2a-1)}{x+1}$,
①当a=0时,h′(x)=-$\frac{x}{x+1}$=0,得x=0,
∵当-1<x<0时,h′(x)>0,当x>0时,h′(x)<0,
∴h(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,
∴x=0是函数h(x)的极大值点,也是方程h(x)=0的唯一解;
②当a≠0时,则h′(x)=$\frac{x(2ax+2a-1)}{x+1}$=0,解得x=0或x=$\frac{1}{2a}$-1,
(i)当a<0时,$\frac{1}{2a}-1<-1$,
∴当-1<x<0时,h′(x)>0,当x>0时,h′(x)<0,
∴h(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,
则x=0是函数h(x)的极大值点,也是方程h(x)=0的唯一解;
(ii)当a>0时,
若a=$\frac{1}{2}$,则h′(x)=$\frac{{x}^{2}}{x+1}≥0$(x>-1),
∴h(x)在(-1,+∞)上单调递增,
∴x=0是方程h(x)=0的唯一解;
若0<a<$\frac{1}{2}$,则h′(x)=0两根x1=0,x2=$\frac{1}{2a}$-1>0,列表如下: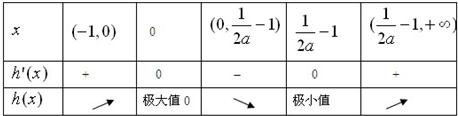
∴h($\frac{1}{2a}$-1)<h(0)=0,而h($\frac{1}{a}$)=$\frac{1}{a}-\frac{1}{a}+ln(\frac{1}{a}+1)$>0,
∴方程h(x)=0在($\frac{1}{2a}-1$,+∞)上还有一解,则h(x)=0解不唯一;
若a>$\frac{1}{2}$,则h′(x)=0两根x1=0,x2=$\frac{1}{2a}-1$∈(-1,0),
同理可得方程h(x)=0在(-1,$\frac{1}{2a}-1$)上还有一解,
则h(x)=0解不唯一,
综上可得,实数a的取值范围是{a|a≤0或a=$\frac{1}{2}$}.
点评 本题考查利用导数研究函数的单调性、最值,导数的几何意义以及图象问题,体现了分类讨论和转化的思想方法.考查了构造法和求导判断函数的单调性的应用,以及学生观察、推理以及创造性地分析问题、解决问题的能力,综合性较强,计算量大,难度较大,对能力要求较高.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案 如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥底面ABCD,∠PCD=90°,PA=AB=AC=2
如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥底面ABCD,∠PCD=90°,PA=AB=AC=2