题目内容
某经销商试销A、B两种商品一个月(30天)的记录如下:
| 日销售量(件) | 0 | 1 | 2 | 3 | 4 | 5 |
| 商品A的频数 | 3 | 5 | 7 | 7 | 5 | 3 |
| 商品B的频数 | 4 | 4 | 6 | 8 | 5 | 3 |
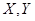 表示售出A、B商品的日利润值(单位:元).将频率视为概率.
表示售出A、B商品的日利润值(单位:元).将频率视为概率.(Ⅰ)设两种商品的销售量互不影响,求两种商品日获利值均超过100元的概率;
(Ⅱ)由于某种原因,该商家决定只选择经销A、B商品的一种,你认为应选择哪种商品,说明理由.
(Ⅰ)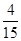 (Ⅱ)应选择经销商品A
(Ⅱ)应选择经销商品A
解析试题分析:(Ⅰ)根据题意求出X、Y的分布列,再求出两种商品日获利值均超过100元的概率;(Ⅱ)先比较X、Y的期望大小,选期望较大者,若相同再比较方差,选方差较小者.
试题解析:(Ⅰ)根据题意,X、Y的分布列如下
P(X>100,Y>100)=(X 0 40 80 120 160 200 Y 0 40 80 120 160 200 P 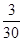
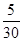
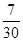
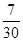
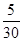
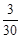
P 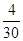
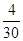
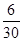
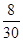
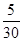
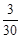
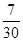 +
+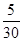 +
+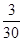 )(
)(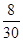 +
+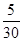 +
+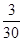 )=
)=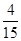 .
.
(Ⅱ)E(X)=0×<

练习册系列答案
相关题目
已知某校在一次考试中,5名学生的数学和物理成绩如下表:
| 学生的编号i | 1 | 2 | 3 | 4 | 5 |
| 数学成绩x | 80 | 75 | 70 | 65 | 60 |
| 物理成绩y | 70 | 66 | 68 | 64 | 62 |
(Ⅱ)根据上表,利用最小二乘法,求出
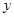 关于
关于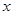 的线性回归方程
的线性回归方程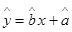 ,
,其中
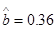
(III)利用(Ⅱ)中的线性回归方程,试估计数学90分的同学的物理成绩.(四舍五入到整数)
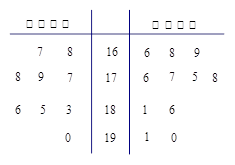
某校高三学生体检后,为了解高三学生的视力情况,该校从高三六个班的300名学生中以班为单位(每班学生50人),每班按随机抽样抽取了8名学生的视力数据.其中高三(1)班抽取的8名学生的视力数据与人数见下表:
| 视力数据 | 4.0 | 4.1 | 4.2 | 4.3 | 4.4 | 4.5 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 | 5.1 | 5.2 | 5.3 |
| 人数 | | | | | 2 | | 2 | | 2 | 1 | | 1 | | |
(2)已知其余五个班学生视力的平均值分别为
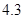 、
、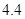 、
、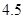 、
、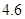 、
、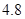 .若从这六个班中任意抽取两个班学生视力的平均值作比较,求抽取的两个班学生视力的平均值之差的绝对值不小于
.若从这六个班中任意抽取两个班学生视力的平均值作比较,求抽取的两个班学生视力的平均值之差的绝对值不小于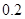 的概率.
的概率. (12分)某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生
(I)分别求出按程序框图正确编程运行时输出y的值为i的概率pi(i=1,2,3);
(II)甲乙两同学依据自己对程序框图的理解,各自编程写出程序重复运行n次后,统计记录输出y的值为i(i=1,2,3)的频数,以下是甲乙所作频数统计表的部分数据.
甲的频数统计图(部分)
| 运行次数n | 输出y的值为1的频数 | 输出y的值为2的频数 | 输出y的值为3的频数 |
| 30 | 14 | 6 | 10 |
| … | … | … | … |
| 2100 | 1027 | 376 | 697 |
| 运行次数n | 输出y的值为1的频数 | 输出y的值为2的频数 | 输出y的值为3的频数 |
| 30 | 12 | 11 | 7 |
| … | … | … | … |
| 2100 | 1051 | 696 | 353 |
(III)将按程序摆图正确编写的程序运行3次,求输出y的值为2的次数ξ的分布列及数学期望.

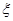 表示乙校中选出的“高个子”人数,试求出
表示乙校中选出的“高个子”人数,试求出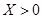 就去打球;若
就去打球;若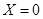 就去唱歌;若
就去唱歌;若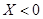 就去下棋.
就去下棋.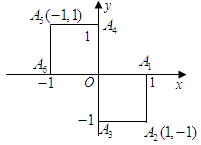
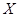 位,若连续抽取到两位愿意购买本地家禽的市民,或抽取的人数达到4位,则停止抽取,求
位,若连续抽取到两位愿意购买本地家禽的市民,或抽取的人数达到4位,则停止抽取,求