题目内容
已知函数 且an=f(n)+f(n+1),
且an=f(n)+f(n+1),
则a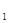 +a
+a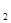 +a
+a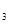 +…+a
+…+a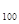 等于 .
等于 .
 且an=f(n)+f(n+1),
且an=f(n)+f(n+1),则a
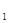 +a
+a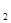 +a
+a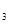 +…+a
+…+a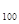 等于 .
等于 .100
解:当n为奇数时,an=f(n)+f(n+1)=n2-(n+1)2=-2n-1,
当n为偶数时,an=f(n)+f(n+1)=-n2+(n+1)2=2n+1,
则S100=(a1+a3+a5+a7+..+a99)+(a2+a4+a6+a8+….+a100)
=-2×(1+3+5+77+..+99)-5+2×(2+4+6+8++…+100)+5
=100
当n为偶数时,an=f(n)+f(n+1)=-n2+(n+1)2=2n+1,
则S100=(a1+a3+a5+a7+..+a99)+(a2+a4+a6+a8+….+a100)
=-2×(1+3+5+77+..+99)-5+2×(2+4+6+8++…+100)+5
=100

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
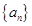 满足
满足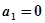 且
且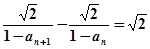 。
。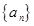 的通项公式;
的通项公式;
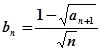 ,记
,记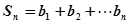 ,证明
,证明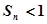 .
. 中,an=n(n-8) -20,这个数列
中,an=n(n-8) -20,这个数列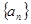
 满足
满足 ,且
,且 ,若数列的前2011项之和为2012,则前2012项的和等于( )
,若数列的前2011项之和为2012,则前2012项的和等于( ) 根据以上规
根据以上规 的通项公式为
的通项公式为 ,则此数列的前
,则此数列的前 项的和等于 ( )
项的和等于 ( )



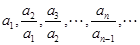 是首项为1,公比为
是首项为1,公比为 的等比数列,则
的等比数列,则 等于( )
等于( )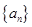 中,
中,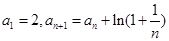 ,则
,则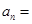
 中,
中, ,
, ,则
,则 的值为( )
的值为( )