题目内容
设等比数列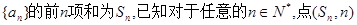 都在函数
都在函数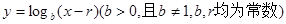 的图象上。
的图象上。
(1)求r的值;
(2)当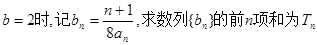 ;
;
(3)若对一切的正整数n,总有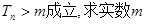 的取值范围。
的取值范围。
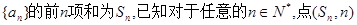 都在函数
都在函数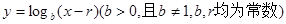 的图象上。
的图象上。(1)求r的值;
(2)当
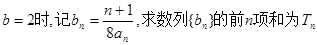 ;
;(3)若对一切的正整数n,总有
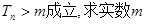 的取值范围。
的取值范围。(1)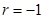 (2)
(2)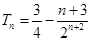 (3)
(3)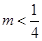
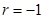 (2)
(2)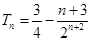 (3)
(3)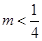
试题分析:(1)由已知可得,

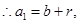 当
当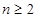 时,
时,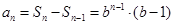
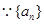 是等比数列,
是等比数列,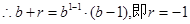 4分
4分(2)由(1)可知,
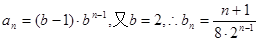
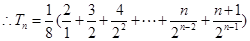
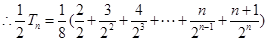
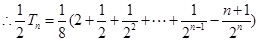
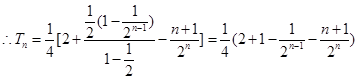
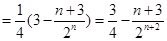 8分
8分(3)
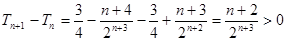
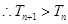
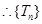 递增,
递增,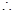 当
当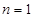 时,
时,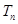 取最小值为
取最小值为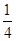
所以一切的
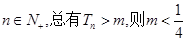 12分
12分点评:数列求和采用的错位相减法,此法适用于通项公式为关于n的一次式与指数式的乘积形式的数列,第三问不等式恒成立转化为求数列前n项和的最值,期间借助了数列的单调性

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 的首项
的首项 前
前 项和为
项和为 ,且
,且
 是等比数列;
是等比数列; ,求函数
,求函数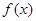 在点
在点 处的导数
处的导数 ,并比较
,并比较 与
与 的大小.
的大小. 满足
满足 ,
, ,且对任意
,且对任意 ,函数
,函数 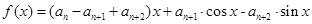 满足
满足
 ,求数列
,求数列 的前
的前 项和
项和 .
. 中,
中,
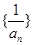 是否为等差数列;
是否为等差数列;
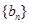 满足
满足 ,求数列
,求数列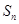 ;
; ,对任意n ≥2的整数恒成立,求实数
,对任意n ≥2的整数恒成立,求实数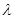 的取值范围.
的取值范围. ,设曲线
,设曲线 在
在 处的切线与
处的切线与 轴交点的纵坐标为
轴交点的纵坐标为 ,则数列
,则数列 的前
的前 的前
的前 项和为
项和为 ,
, ,
, ,,则
,,则 ( )
( )



 首项
首项 ,公差为
,公差为 ,且数列
,且数列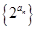 是公比为4的等比数列,
是公比为4的等比数列, 及前
及前 项和
项和 ;
;  的前
的前 .
.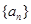 的前
的前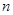 项的和为
项的和为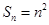 ,则
,则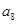 =_________.
=_________.