题目内容
知数列 的首项
的首项 前
前 项和为
项和为 ,且
,且
(1)证明:数列 是等比数列;
是等比数列;
(2)令 ,求函数
,求函数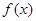 在点
在点 处的导数
处的导数 ,并比较
,并比较 与
与 的大小.
的大小.
 的首项
的首项 前
前 项和为
项和为 ,且
,且
(1)证明:数列
 是等比数列;
是等比数列;(2)令
 ,求函数
,求函数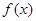 在点
在点 处的导数
处的导数 ,并比较
,并比较 与
与 的大小.
的大小.(1)详见解析;(2) ; 当
; 当 时,
时, ; 当
; 当 时,
时, ;当
;当 时,
时,

 .
.
 ; 当
; 当 时,
时, ; 当
; 当 时,
时, ;当
;当 时,
时,

 .
.试题分析:(1)先利用
 与
与 的递推关系得到
的递推关系得到 与
与 的递推关系式,再通过构造新数列,并结合等比数列的定义来证明
的递推关系式,再通过构造新数列,并结合等比数列的定义来证明 是等比数列;(2)先求导得到
是等比数列;(2)先求导得到 的表达式,然后分组求和,一部分是用错位相减法,另一部分是用等差数列求和公式,最后通过作差比较
的表达式,然后分组求和,一部分是用错位相减法,另一部分是用等差数列求和公式,最后通过作差比较 与
与 的大小情况.
的大小情况.试题解析:(1)由已知
 ,可得
,可得 两式相减得
两式相减得 即
即 从而
从而 4分
4分当
 时
时 所以
所以 又
又 所以
所以 从而
从而 5分
5分故总有
 ,
, 又
又
从而
 即数列
即数列 是等比数列; 6分
是等比数列; 6分(2)由(1)知
 ,因为
,因为 所以
所以
从而
 =
=
=


令
 ,
,

错位相减得,

 10分
10分由上

 =
= =12
=12 ①
①当
 时,①式=0所以
时,①式=0所以 ;
;当
 时,①式=12
时,①式=12 所以
所以
当
 时,
时, 又由函数
又由函数 可
可
所以
 即①
即① 从而
从而

 14分
14分 项和的求法,3、函数的求导.
项和的求法,3、函数的求导.
练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
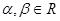 且
且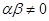 ,数列
,数列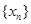 满足
满足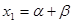 ,
,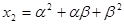 ,
,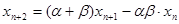 (
(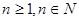 ),令
),令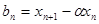 ,
,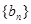 是等比数列;
是等比数列;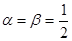 ,求
,求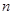 项和
项和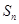 .
. 的前
的前 项和
项和 ,满足:
,满足: .
. ;
; 的满足
的满足 ,
, 为数列
为数列 的前
的前 .
.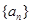 的前
的前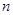 项和为
项和为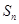 ,且满足
,且满足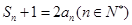 .
.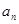 与
与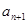 两项之间插入
两项之间插入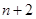 个数构成等差数列,其公差为
个数构成等差数列,其公差为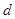 ,求数列
,求数列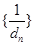 的前
的前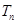 .
.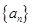 ,其前
,其前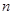 项的和为
项的和为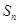 ,且
,且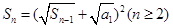 ,若
,若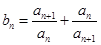 ,且数列
,且数列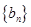 的前
的前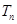 ,则
,则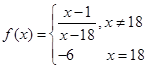 ,则
,则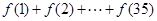 的值为 .
的值为 . 的前n项和
的前n项和 ,则( )
,则( )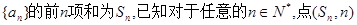 都在函数
都在函数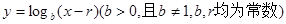 的图象上。
的图象上。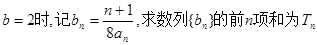 ;
;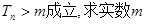 的取值范围。
的取值范围。 满足:
满足: ,数列
,数列 满足
满足 .
. 求
求 的值及
的值及 的等比数列,问是否存在正实数
的等比数列,问是否存在正实数 ,使得数列
,使得数列 的前
的前 项和
项和 (用n,
(用n, 表示).
表示).