题目内容
在△ABC中,内角A,B,C所对的边分别为a,b,c,cos B=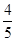 .
.
(1)求cos(A+C)的值;
(2)求sin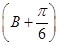 的值;
的值;
(3)若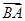 ·
·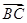 =20,求△ABC的面积.
=20,求△ABC的面积.
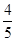 .
.(1)求cos(A+C)的值;
(2)求sin
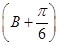 的值;
的值;(3)若
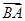 ·
·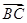 =20,求△ABC的面积.
=20,求△ABC的面积.(1)-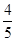 (2)
(2) (3)
(3)
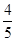 (2)
(2) (3)
(3)
(1)在△ABC中,∵A+B+C=π,∴A+C=π-B.
∵cos B=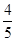 ,∴cos(A+C)=cos(π-B)=-cos B=-
,∴cos(A+C)=cos(π-B)=-cos B=-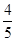 .
.
(2)在△ABC中,∵cos B=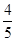 ,∴sin B=
,∴sin B= =
= ,
,
∴sin(B+ )=sin Bcos
)=sin Bcos +cos Bsin
+cos Bsin =
= ×
×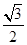 +
+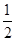 ×
×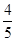 =
= .
.
(3)∵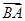 ·
·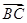 =20,即|
=20,即|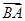 |·|
|·|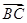 |cos B=20,
|cos B=20,
∴c·a·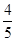 =20,即ac=25.
=20,即ac=25.
∴△ABC的面积S△ABC=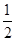 acsin B=
acsin B=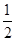 ×25×
×25× =
=
∵cos B=
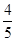 ,∴cos(A+C)=cos(π-B)=-cos B=-
,∴cos(A+C)=cos(π-B)=-cos B=-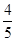 .
.(2)在△ABC中,∵cos B=
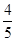 ,∴sin B=
,∴sin B= =
= ,
,∴sin(B+
 )=sin Bcos
)=sin Bcos +cos Bsin
+cos Bsin =
= ×
×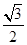 +
+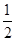 ×
×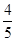 =
= .
.(3)∵
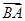 ·
·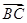 =20,即|
=20,即|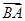 |·|
|·|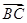 |cos B=20,
|cos B=20,∴c·a·
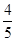 =20,即ac=25.
=20,即ac=25.∴△ABC的面积S△ABC=
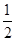 acsin B=
acsin B=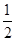 ×25×
×25× =
=

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 ,△EFC的面积为
,△EFC的面积为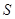 .
.

 求
求 的值域;
的值域; 求
求 的值.
的值.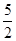
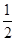

 b,且a>b,则∠B等于( )
b,且a>b,则∠B等于( )
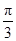



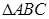 的内角
的内角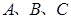 的对边分别为
的对边分别为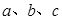 ,若
,若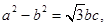
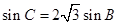 ,则
,则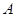 =______.
=______. absin C,则△ABC的形状是( )
absin C,则△ABC的形状是( ) 的内角
的内角 满足
满足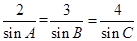 ,则
,则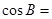 ( )
( )