Question

【题目】如图，已知四棱锥P-ABCD，底面，且底面ABCD是边长为2的正方形，M、N分别为PB、PC的中点.

（1）证明：MN//平面PAD；

（2）若PA与平面ABCD所成的角为，求四棱锥P-ABCD的体积V.

Answer 1

【答案】（1）详见解析（2）

【解析】

试题分析：（I）由中位线定理得出MN∥BC，由MN∥AD，故MN∥AD，得出MN∥平面PAD；（II）由∠PAD=45°得出PD=AD，于是棱锥体积V=S正方形ABCDPD

试题解析：（1）证明：因为M、N分别是棱PB、PC中点，所以MN//BC，

又 ABCD是正方形，所以AD// BC，于是MN//AD. 3分

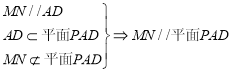6分

（2）由，知PA与平面ABCD所成的角为，

∴ 9分

在中，知，

故四棱锥P-ABCD的体积. 12分