题目内容
【题目】如图,已知长方体ABCD﹣A1B1C1D1中,E,M,N分别是BC,AE,CD1的中点,AD=AA1=a,AB=2a.求证:MN∥平面ADD1A1 . 
【答案】证明:以D为原点,分别以DA、DC、DD1为x轴、y轴、z轴建立空间直角坐标系,则A(a,0,0),B(a,2a,0),C(0,2a,0),D1(0,0,a),E( ![]() a,2a,0),
a,2a,0), 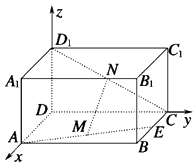
∵M、N分别为AE、CD1的中点,
∴M( ![]() a,a,0),N(0,a,
a,a,0),N(0,a, ![]() ).
).
∴ ![]() =(﹣
=(﹣ ![]() a,0,
a,0, ![]() ).
).
取 ![]() =(0,1,0),
=(0,1,0),
显然 ![]() =⊥平面A1D1DA,且
=⊥平面A1D1DA,且 ![]()
![]() =0,
=0,
∴ ![]() ⊥
⊥ ![]() .又MN平面ADD1A1 .
.又MN平面ADD1A1 .
∴MN∥平面ADD1A1
【解析】以D为原点,分别以DA、DC、DD1为x轴、y轴、z轴建立空间直角坐标系,求出 ![]() =(﹣
=(﹣ ![]() a,0,
a,0, ![]() ).平面ADD1A1的法向量
).平面ADD1A1的法向量 ![]() =(0,1,0),通过
=(0,1,0),通过 ![]()
![]() =0,证明MN∥平面ADD1A1 .
=0,证明MN∥平面ADD1A1 .
【考点精析】关于本题考查的直线与平面平行的判定,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能得出正确答案.

练习册系列答案
相关题目
