Question

【题目】已知f（x）是定义在R上的且以2为周期的偶函数，当0≤x≤1时，f（x）=x2 ， 如果直线y=x+a与曲线y=f（x）恰有两个不同的交点，则实数a的值为（ ）
A.2k（k∈Z）
B.2k或2k+ （k∈Z）
C.0
D.2k或2k﹣ （k∈Z）

Answer 1

【答案】D
【解析】解：设﹣1≤x≤0，则 0≤﹣x≤1，f（﹣x）=（﹣x）2=x2=f（x），
综上，f（x）=x2 ， x∈[﹣1，1]，f（x）=（x﹣2k）2 ， x∈[2k﹣1，2k+1]，
由于直线y=x+a的斜率为1，在y轴上的截距等于a，在一个周期[﹣1，1]上，
a=0时 满足条件，a=﹣ 时，在此周期上直线和曲线相切，
并和曲线在下一个区间上图象
有一个交点，也满足条件． 由于f（x）的周期为2，
故在定义域内，满足条件的a 应是 2k+0 或 2k﹣ ，k∈Z．
故选 D．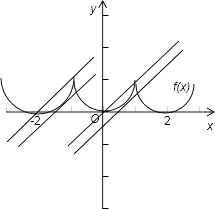

【考点精析】关于本题考查的函数奇偶性的性质，需要了解在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇才能得出正确答案．