题目内容
在△ABC中,角A、B、C的对边分别是 .已知
.已知
(1)求角C的大小;
(2)若 ,求△ABC外接圆半径.
,求△ABC外接圆半径.
(1) (2)
(2)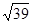 .
.
解析试题分析:(1)由三角函数给值求角知识可知:要求角的大小,首先必须明确角的范围,再就是求出角的某一三角函数值;因此既然是求角C,而已知等式 中只含有角C,所以只须将cosC移到等式的右侧,逆用余弦倍角公式,左边用正弦的倍角公式化成
中只含有角C,所以只须将cosC移到等式的右侧,逆用余弦倍角公式,左边用正弦的倍角公式化成 再注意到
再注意到 ,从而可得
,从而可得 ,然后两边一平方就可求得sinC=
,然后两边一平方就可求得sinC= ,但不能就此得到角C为
,但不能就此得到角C为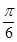 ,还必须注意到
,还必须注意到 ,所以
,所以 (2)由正弦定理可知:△ABC外接圆半径R满足
(2)由正弦定理可知:△ABC外接圆半径R满足 ,由(1)知角C的大小,所以只需求出边c即可;注意观察已知等式
,由(1)知角C的大小,所以只需求出边c即可;注意观察已知等式 知可分别按边a,b配方得到
知可分别按边a,b配方得到 从而得到
从而得到 再用余弦定理
再用余弦定理 就可求出边c,进而就可求得三角形的外接圆半径.
就可求出边c,进而就可求得三角形的外接圆半径.
试题解析:(1)∵ 即
即
由 ,∴
,∴ ,即
,即
∵ ,得
,得 即
即 ,所以
,所以
(2)由 得
得 得
得
∴ ∴
∴ .
.
考点:1.三角公式;2.正弦定理和余弦定理.

练习册系列答案
相关题目

 ,设S为△ABC的面积,且
,设S为△ABC的面积,且 。
。 ,求△ABC周长的取值范围.
,求△ABC周长的取值范围. 中,内角
中,内角 的对边分别为
的对边分别为 .
. 的度数;
的度数;  求
求 ,
, ,若
,若
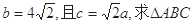 的面积.
的面积. ,求△ABC的面积.
,求△ABC的面积.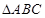 中,BD为
中,BD为 的平分线,已知
的平分线,已知 ,
, _____________;
_____________;  上的奇函数,且在区间(0,
上的奇函数,且在区间(0, )上单调递增,若
)上单调递增,若 ,三
,三 角形的内角A满足
角形的内角A满足 ,则A的取值范围是
,则A的取值范围是