题目内容
在△ABC中,角A,B,C所对的边分别为 ,设S为△ABC的面积,且
,设S为△ABC的面积,且 。
。
(Ⅰ)求角A的大小;
(Ⅱ)若 ,求△ABC周长的取值范围.
,求△ABC周长的取值范围.
(1)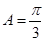 ;(2)周长的取值范围是
;(2)周长的取值范围是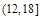 .
.
解析试题分析:(1)在解决三角形的问题中,面积公式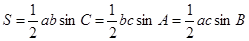 最常用,因为公式中既有边又有角,容易和正弦定理、余弦定理联系起来;(2)在三角形中,两边和一角知道,该三角形是确定的,其解是唯一的,利用余弦定理求第三边.(3)若是已知两边和一边的对角,该三角形具有不唯一性,通常根据大边对大角进行判断.(4)在三角形中,注意
最常用,因为公式中既有边又有角,容易和正弦定理、余弦定理联系起来;(2)在三角形中,两边和一角知道,该三角形是确定的,其解是唯一的,利用余弦定理求第三边.(3)若是已知两边和一边的对角,该三角形具有不唯一性,通常根据大边对大角进行判断.(4)在三角形中,注意 这个隐含条件的使用,在求范围时,注意根据题中条件限制角的范围.
这个隐含条件的使用,在求范围时,注意根据题中条件限制角的范围.
试题解析:解:(Ⅰ)由题意可知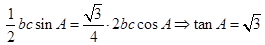 ,
,
所以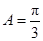 4分
4分
(Ⅱ)法一:由已知: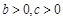 ,
,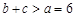
由余弦定理得: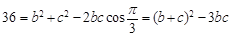
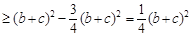
(当且仅当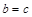 时等号成立)
时等号成立)
∴(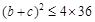 ,又
,又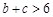 , ∴
, ∴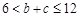 ,
,
从而周长的取值范围是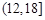 . 12分
. 12分
法二:由正弦定理得: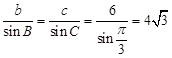
∴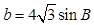 ,
,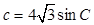 ,
,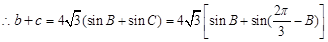
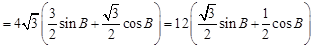
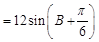 .
.
∵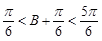
∴ ,即
,即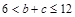 (当且仅当
(当且仅当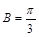 时,等号成立)
时,等号成立)
从而周长的取值范围是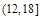 12分
12分
考点:(1)与面积有关的问题;(2)求三角形周长的范围.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
已知 ABC外接圆O的半径为1,且
ABC外接圆O的半径为1,且  ,从圆O内随机取一个点M,若点M取自△ABC内的概率恰为
,从圆O内随机取一个点M,若点M取自△ABC内的概率恰为 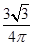 ,则
,则 MBC的形状为
MBC的形状为
| A.直角三角形 | B.等边三角形 | C.钝角三角形 | D.等腰直角三角形 |
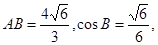 点D、E分别为AC、BC边的中点,且BD=
点D、E分别为AC、BC边的中点,且BD= ,
, .已知
.已知
 ,求△ABC外接圆半径.
,求△ABC外接圆半径. 中,角
中,角 对的边分别为
对的边分别为 ,且
,且 .
. 的值;
的值; ,求
,求 .
. 的三个内角
的三个内角 成等差数列,它们的对边分别为
成等差数列,它们的对边分别为 ,且满足
,且满足 ,
, .
. ;
; .
. 中,角
中,角 所对的边分别为
所对的边分别为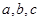 ,且
,且 是方程
是方程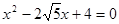 的两个根,且
的两个根,且 ,求:
,求: 的度数; (2)边
的度数; (2)边 的长度.
的长度. 中,角
中,角 所对的边分别为
所对的边分别为 ,若
,若 ,b=
,b= ,
, ,则
,则 .
.  分别是
分别是 的三个内角
的三个内角 所对的边,若
所对的边,若 且
且 是
是  与
与 的等差中项,则
的等差中项,则 =
=