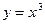题目内容
(本小题满分14分)
 如图,已知圆
如图,已知圆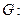
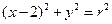 是椭圆
是椭圆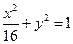 的内接△
的内接△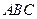 的内切圆, 其中
的内切圆, 其中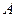 为椭圆的左顶点.
为椭圆的左顶点.
(1)求圆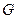 的半径
的半径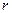 ;
;
(2)过点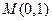 作圆
作圆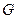 的两条切线交椭圆于
的两条切线交椭圆于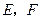 两点,
两点,
证明:直线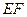 与圆
与圆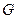 相切.
相切.
 如图,已知圆
如图,已知圆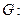
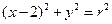 是椭圆
是椭圆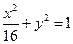 的内接△
的内接△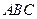 的内切圆, 其中
的内切圆, 其中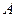 为椭圆的左顶点.
为椭圆的左顶点. (1)求圆
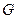 的半径
的半径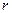 ;
;(2)过点
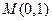 作圆
作圆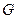 的两条切线交椭圆于
的两条切线交椭圆于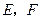 两点,
两点,
|
|
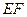 与圆
与圆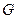 相切.
相切. 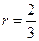
(1)解设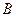
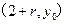 ,过圆心
,过圆心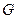 作
作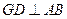 于
于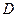 ,
, 交长轴于
交长轴于
由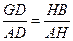 得
得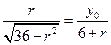 ,
,
即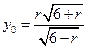 (1)
(1)
而点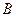
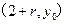 在椭圆上,
在椭圆上,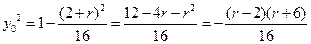 (2)
(2)
由(1)、 (2)式得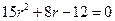 ,解得
,解得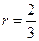 或
或 (舍去)
(舍去)
(2) 证明设过点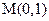 与圆
与圆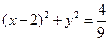 相切的直线方程为:
相切的直线方程为:
 (3)
(3)
则 ,即
,即 (4)
(4)
解得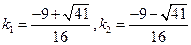
将(3)代入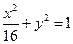 得
得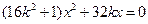 ,则异于零的解为
,则异于零的解为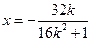
设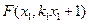 ,
,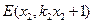 ,则
,则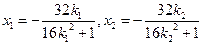
则直线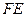 的斜率为:
的斜率为:
于是直线 的方程为:
的方程为: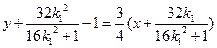
即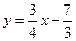
则圆心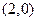 到直线
到直线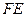 的距离
的距离

 故结论成立.
故结论成立.
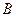
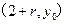 ,过圆心
,过圆心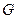 作
作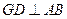 于
于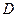 ,
, 交长轴于
交长轴于
由
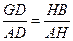 得
得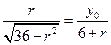 ,
,即
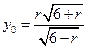 (1)
(1) 而点
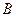
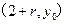 在椭圆上,
在椭圆上,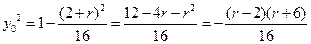 (2)
(2)由(1)、 (2)式得
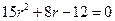 ,解得
,解得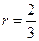 或
或 (舍去)
(舍去)(2) 证明设过点
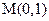 与圆
与圆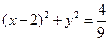 相切的直线方程为:
相切的直线方程为: (3)
(3)则
 ,即
,即 (4)
(4)解得
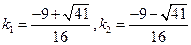
将(3)代入
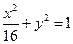 得
得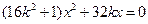 ,则异于零的解为
,则异于零的解为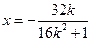
设
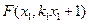 ,
,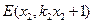 ,则
,则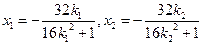
则直线
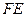 的斜率为:
的斜率为:
于是直线
 的方程为:
的方程为: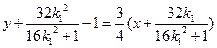
即
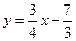
则圆心
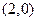 到直线
到直线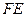 的距离
的距离

 故结论成立.
故结论成立.
练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
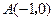 ,
, ,动点
,动点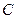 满足
满足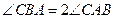 ,求动点
,求动点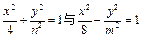 有相同的准线,则动点P (n, m)的轨迹为
有相同的准线,则动点P (n, m)的轨迹为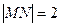 ,点P为线段MN的中点。
,点P为线段MN的中点。 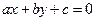 与上述轨迹交于A.B两点,且
与上述轨迹交于A.B两点,且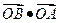 ,求:
,求: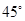 的直线
的直线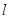 过点
过点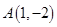 和点
和点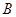 ,点
,点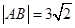 。
。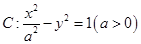 相交于
相交于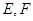 两点,且线段
两点,且线段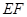 的中点坐标为
的中点坐标为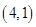 ,求
,求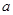 的值;
的值;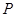 ,当点
,当点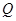 在线段
在线段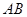 上运动时,称
上运动时,称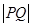 的最小值为
的最小值为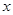 轴上运动,写出点
轴上运动,写出点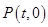 到线段
到线段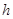 关于
关于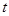 的函数关系式。
的函数关系式。 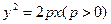 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.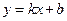 与抛物线C交于两点
与抛物线C交于两点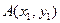 ,
,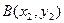 ,且
,且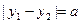 (
(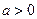 ,且
,且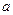 为常数).过弦AB的中点M作平行于
为常数).过弦AB的中点M作平行于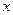 轴的直线交抛物线于点D,连结AD、 BD得到
轴的直线交抛物线于点D,连结AD、 BD得到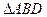 .
.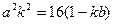 ;
;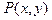

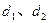

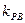 和
和