题目内容
2.设m,n为正实数,且m+n=1,则$\frac{1}{m}+\frac{1}{n}$的最小值是4.分析 由题意可得$\frac{1}{m}+\frac{1}{n}$=($\frac{1}{m}+\frac{1}{n}$)(m+n)=2+$\frac{n}{m}$+$\frac{m}{n}$,由基本不等式可得.
解答 解:∵m,n为正实数,且m+n=1,
∴$\frac{1}{m}+\frac{1}{n}$=($\frac{1}{m}+\frac{1}{n}$)(m+n)
=2+$\frac{n}{m}$+$\frac{m}{n}$≥2+2$\sqrt{\frac{n}{m}•\frac{m}{n}}$=4
当且仅当$\frac{n}{m}$+$\frac{m}{n}$即m=n=$\frac{1}{2}$时取等号,
∴$\frac{1}{m}+\frac{1}{n}$的最小值为:4
故答案为:4
点评 本题考查基本不等式求最值,属基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
12.如图所示,程序执行后的输出结果为( )
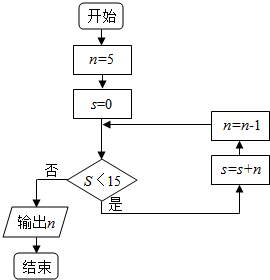

| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
13.已知实数x,y满足不等式组$\left\{{\begin{array}{l}{2x-y+2≥0}\\{x+y-2≥0}\\{x≤2}\end{array}}\right.$,则$\frac{y-1}{x+3}$的取值范围是( )
| A. | $(-∞,-\frac{1}{5}]∪[1,+∞)$ | B. | $[\frac{1}{3},1]$ | C. | [-$\frac{1}{5}$,$\frac{1}{3}$] | D. | [-$\frac{1}{5}$,1] |
7.若(1+ai)i=2-bi,其中a、b∈R,i是虚数单位,则|a+bi|=( )
| A. | $\sqrt{5}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 3 |