题目内容
设函数f(x)=
,g(x)=f(x)-ax,x∈[1,3],其中a∈R,记函数g(x)的最大值与最小值的差为h(a).
(Ⅰ)求函数h(a)的解析式;
(Ⅱ)画出函数y=h(x)的图象并指出h(x)的最小值.
|
(Ⅰ)求函数h(a)的解析式;
(Ⅱ)画出函数y=h(x)的图象并指出h(x)的最小值.
考点:函数的最值及其几何意义,分段函数的应用
专题:函数的性质及应用
分析:(Ⅰ)根据题意先求出函数g(x)的解析式,再由一次函数的单调性和x的范围对a进程分类讨论,利用一次函数的单调性以及端点处的函数值,分别求出函数的最大值、最小值,再求出最大值与最小值的差为h(a),最后用分段函数的形式表示出来;
(Ⅱ)根据h(a)的解析式画出函数图象,由图求出h(x)的最小值.
(Ⅱ)根据h(a)的解析式画出函数图象,由图求出h(x)的最小值.
解答:
解:(I)由题意得,g(x)=
,
(1)当a<0时,函数g(x)是[1,3]增函数,
此时,g(x)max=g(3)=2-3a,g(x)min=g(1)=1-a,所以h(a)=1-2a;
(2)当a>1时,函数g(x)是[1,3]减函数,此时,g(x)min=g(3)=2-3a,g(x)max=g(1)=1-a,所以h(a)=2a-1;
(3)当0≤a≤1时,若x∈[1,2],则g(x)=1-ax,有g(2)≤g(x)≤g(1);
若x∈[2,3],则g(x)=(1-a)x-1,有g(2)≤g(x)≤g(3);
因此,g(x)min=g(2)=1-2a,而g(3)-g(1)=(2-3a)-(1-a)=1-2a,
故当0≤a≤
时,g(x)max=g(3)=2-3a,有h(a)=1-a;
当
<a≤1时,g(x)max=g(1)=1-a,有h(a)=a;
综上所述:h(a)=
.
(II)画出y=h(x)的图象,如右图.
数形结合,可得h(x)min=h(
)=
.
|
(1)当a<0时,函数g(x)是[1,3]增函数,
此时,g(x)max=g(3)=2-3a,g(x)min=g(1)=1-a,所以h(a)=1-2a;
(2)当a>1时,函数g(x)是[1,3]减函数,此时,g(x)min=g(3)=2-3a,g(x)max=g(1)=1-a,所以h(a)=2a-1;
(3)当0≤a≤1时,若x∈[1,2],则g(x)=1-ax,有g(2)≤g(x)≤g(1);
若x∈[2,3],则g(x)=(1-a)x-1,有g(2)≤g(x)≤g(3);

因此,g(x)min=g(2)=1-2a,而g(3)-g(1)=(2-3a)-(1-a)=1-2a,
故当0≤a≤
| 1 |
| 2 |
当
| 1 |
| 2 |
综上所述:h(a)=
|
(II)画出y=h(x)的图象,如右图.
数形结合,可得h(x)min=h(
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查分段函数的最值,以及函数的单调性与图象的应用,考查分类讨论思想、数形结合思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知
、
、
是不共面的三个向量,则下列向量组能作为一个基底的是( )
| a |
| b |
| c |
A、2
| ||||||||||
B、2
| ||||||||||
C、
| ||||||||||
D、
|
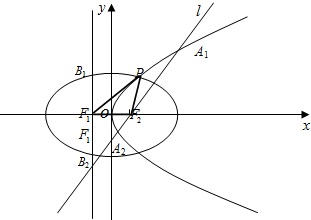 如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1、F2为焦点,离心率e=
如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1、F2为焦点,离心率e=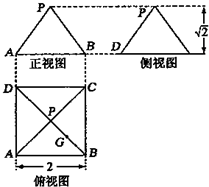 某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.