题目内容
如右图,在棱长为a的正方体ABCDA1B1C1D1中,G为△BC1D的重心,
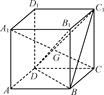
(1)试证:A1、G、C三点共线;
(2)试证:A1C⊥平面BC1D;

(1)试证:A1、G、C三点共线;
(2)试证:A1C⊥平面BC1D;
(1)见解析(2)见解析
(1)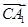 =
=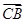 +
+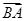 +
+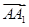 =
=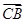 +
+ +
+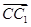 ,
,
可以证明: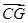 =
=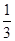 (
(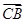 +
+ +
+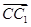 )=
)=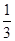
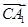 ,
,
∴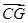 ∥
∥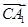 ,即A1、G、C三点共线.
,即A1、G、C三点共线.
(2)设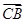 =a,
=a, =b,
=b,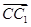 =c,则|a|=|b|=|c|=a,且a·b=b·c=c·a=0,
=c,则|a|=|b|=|c|=a,且a·b=b·c=c·a=0,
∵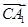 =a+b+c,
=a+b+c,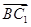 =c-a,
=c-a,
∴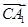 ·
·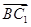 =(a+b+c)·(c-a)=c2-a2=0,
=(a+b+c)·(c-a)=c2-a2=0,
∴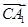 ⊥
⊥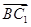 ,即CA1⊥BC1,
,即CA1⊥BC1,
同理可证:CA1⊥BD,因此A1C⊥平面BC1D.
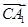 =
=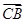 +
+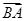 +
+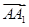 =
=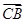 +
+ +
+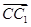 ,
,可以证明:
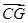 =
=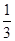 (
(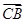 +
+ +
+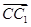 )=
)=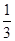
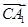 ,
,∴
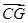 ∥
∥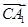 ,即A1、G、C三点共线.
,即A1、G、C三点共线.(2)设
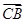 =a,
=a, =b,
=b,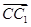 =c,则|a|=|b|=|c|=a,且a·b=b·c=c·a=0,
=c,则|a|=|b|=|c|=a,且a·b=b·c=c·a=0,∵
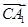 =a+b+c,
=a+b+c,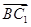 =c-a,
=c-a,∴
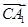 ·
·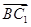 =(a+b+c)·(c-a)=c2-a2=0,
=(a+b+c)·(c-a)=c2-a2=0,∴
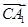 ⊥
⊥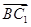 ,即CA1⊥BC1,
,即CA1⊥BC1,同理可证:CA1⊥BD,因此A1C⊥平面BC1D.

练习册系列答案
相关题目
 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱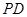 ⊥底面
⊥底面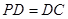 ,
, 是
是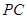 的中点,作
的中点,作 交
交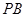 于点
于点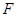 .
.
 平面
平面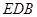 ;
;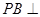 平面
平面 .
.
 AB.
AB.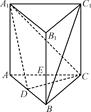
 所在的平面和平面
所在的平面和平面 互相垂直,等腰梯形
互相垂直,等腰梯形 ∥
∥ ,
,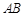 =2,
=2,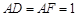 ,
, ,
,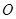 ,
,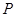 分别为
分别为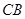 的中点,
的中点,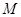 为底面
为底面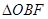 的重心.
的重心.
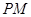 ∥平面
∥平面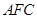 ;
;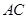 与平面
与平面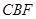 所成角的正弦值.
所成角的正弦值.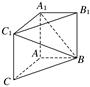
 的值.
的值.