题目内容
某地政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知 其中AF是以A为顶点、AD为对称轴的抛物线段.试求该高科技工业园区的最大面积.
其中AF是以A为顶点、AD为对称轴的抛物线段.试求该高科技工业园区的最大面积.

解析试题分析:求该高科技工业园区的最大面积,由梯形的面积公式须知PQ,PR,QE的长度,注意到点P在曲线AF上的动点,因此此题可建立直角坐标系求解,故以A为原点,AB所在的直线为x轴建立直角坐标系,从而得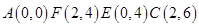 ,而曲线AF是以A为定点,AD为对称轴的抛物线段,故利用AF求出抛物线的方程,利用EC求出直线EC的方程,设出P点的坐标为
,而曲线AF是以A为定点,AD为对称轴的抛物线段,故利用AF求出抛物线的方程,利用EC求出直线EC的方程,设出P点的坐标为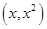 ,从而得出PQ,PR,PE的长度,由梯形的面积公式,得出工业园区的面积
,从而得出PQ,PR,PE的长度,由梯形的面积公式,得出工业园区的面积
 ,由于是三次函数,需用求导来求最大值,从而解出高科技工业园区的最大面积是
,由于是三次函数,需用求导来求最大值,从而解出高科技工业园区的最大面积是 .
.
试题解析:以A为原点,AB所在直线为x轴建立直角坐标系如图,则 …(2分)
…(2分)
由题意可设抛物线段所在抛物线的方程为 ,由
,由 得,
得, ,
,
∴AF所在抛物线的方程为 , (5分)
, (5分)
又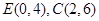 ,∴EC所在直线的方程为
,∴EC所在直线的方程为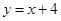 ,
,
设 ,则
,则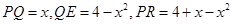 , (9分)
, (9分)
∴工业园区的面积
 , (12分)
, (12分)
∴ 令
令 得
得 或
或 (舍去负值) , (13分)
(舍去负值) , (13分)
当 变化时,
变化时, 和
和 的变化情况可知,当
的变化情况可知,当 时,
时, 取得最大值
取得最大值 .
.
答:该高科技工业园区的最大面积 .
.
考点:平面解析几何与导数的应用.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 的导函数为
的导函数为 ,
, 的图象在点
的图象在点 ,
, 处的切线方程为
处的切线方程为 ,且
,且 ,直线
,直线 是函数
是函数 的图象的一条切线.
的图象的一条切线. 的值;
的值; 对于任意
对于任意 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,
,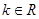 .
. ,求函数
,求函数 的单调区间;
的单调区间;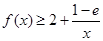 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,若对任意的两个实数
,若对任意的两个实数 满足
满足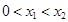 ,总存在
,总存在 ,使得
,使得
 成立,证明:
成立,证明: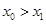 .
. (f′(x)是f(x)的导函数)在区间(t,3)上总不是单调函数,求m的取值范围;
(f′(x)是f(x)的导函数)在区间(t,3)上总不是单调函数,求m的取值范围; ×…×
×…× <
< (n≥2,n∈N*)
(n≥2,n∈N*)
 的最小值;
的最小值; ,
, .
. 时,
时, 的图象与
的图象与 的图象有唯一的公共点;
的图象有唯一的公共点; 时,
时, 的取值范围.
的取值范围. .
. .的单调区间;
.的单调区间; 的极值.
的极值. 上的函数
上的函数 同时满足以下条件:
同时满足以下条件: 在(0,1)上是减函数,在(1,+∞)上是增函数;
在(0,1)上是减函数,在(1,+∞)上是增函数; 是偶函数;
是偶函数; y=x+2垂直.
y=x+2垂直. =
= ,若存在实数x∈[1,e],使
,若存在实数x∈[1,e],使 <
< 在
在 及
及 时取得极值.
时取得极值. ,都有
,都有 成立,求c的取值范围.
成立,求c的取值范围.