题目内容
已知函数 .
.
(1)求函数 .的单调区间;
.的单调区间;
(2)设函数 的极值.
的极值.
(1) 函数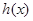 的单调增区间为
的单调增区间为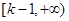 ,单调减区间为
,单调减区间为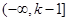
(2) 当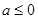 时,
时,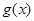 无极值;当
无极值;当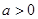 ,
,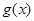 在
在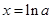 处取得极小值
处取得极小值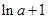 ,无极大值。
,无极大值。
解析试题分析:(1) 求单调区间只需解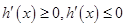 不等式即可;
不等式即可;
(2) 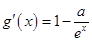 ,在求极值时要对参数
,在求极值时要对参数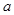 讨论,显然当
讨论,显然当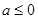 时
时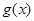 为增函数,无极值,当
为增函数,无极值,当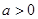 时可求得
时可求得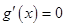 的根,再讨论两侧的单调性;判断极值的方法是先求得
的根,再讨论两侧的单调性;判断极值的方法是先求得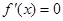 的根,再看在每个根的两侧导函数的正负是否一致,只有两侧导函数的符号不一样才能确定这个根是极值点.这个判断过程通常要放在一个表格中去体现.
的根,再看在每个根的两侧导函数的正负是否一致,只有两侧导函数的符号不一样才能确定这个根是极值点.这个判断过程通常要放在一个表格中去体现.
试题解析:(1) 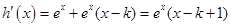
当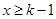 时,
时, 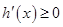 ,
,
当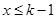 时,
时, 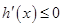 ,
,
故函数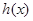 的单调增区间为
的单调增区间为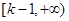 ,单调减区间为
,单调减区间为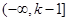 .
.
(2) 由题意: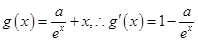
①当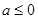 时,
时,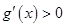 ,
,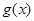 为
为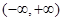 上的增函数,所以
上的增函数,所以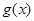 无极值。
无极值。
②当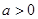 时,令
时,令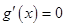 得,
得,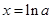
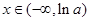 ,
,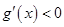 ;
;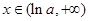 ,
,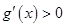
所以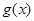 在
在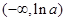 上单调递减,在
上单调递减,在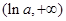 上单调递增
上单调递增
所以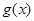 在
在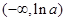 处取得极小值,且极小值为
处取得极小值,且极小值为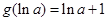 ,无极大值
,无极大值
综上,当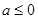 时,
时,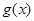 无极值;当
无极值;当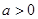 ,
,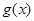 在
在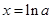 处取得极小值
处取得极小值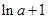 ,无极大值。
,无极大值。
考点:1、函数的单调区间;2、函数的极值.

练习册系列答案
相关题目

 存在极大值和极小值,求
存在极大值和极小值,求 的取值范围;
的取值范围; 分别为
分别为 的极大值和极小值,其中
的极大值和极小值,其中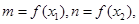 且
且 求
求 的取值范围.
的取值范围. 其中AF是以A为顶点、AD为对称轴的抛物线段.试求该高科技工业园区的最大面积.
其中AF是以A为顶点、AD为对称轴的抛物线段.试求该高科技工业园区的最大面积.
 是曲线
是曲线
 的一条切线,
的一条切线,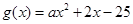 .
. 的值;
的值; 时,存在
时,存在
 ,求实数
,求实数 的取值范围.
的取值范围.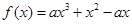 ,其中
,其中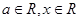 .
. 时,求函数
时,求函数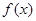 在
在 处的切线方程;
处的切线方程; 的取值范围;
的取值范围;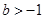 ,如果存在
,如果存在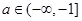 ,使得函数
,使得函数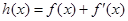
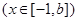 在
在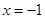 处取得最小值,试求
处取得最小值,试求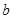 的最大值.
的最大值. 为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为
为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为 ,对称轴与地面垂直,沟深2米,沟中水深1米.
,对称轴与地面垂直,沟深2米,沟中水深1米.

 ,
, .
. ,则
,则 ,
, 满足什么条件时,曲线
满足什么条件时,曲线 与
与 在
在 处总有相同的切线?
处总有相同的切线? 时,求函数
时,求函数 的单调减区间;
的单调减区间; 时,若
时,若 对任意的
对任意的 恒成立,求
恒成立,求 .
. ,函数
,函数 在区间
在区间 上是单调递增函数,求实数
上是单调递增函数,求实数 的取值范围;
的取值范围; ,若对任意
,若对任意 恒成立,求
恒成立,求