题目内容
已知函数 的导函数为
的导函数为 ,
, 的图象在点
的图象在点 ,
, 处的切线方程为
处的切线方程为 ,且
,且 ,直线
,直线 是函数
是函数 的图象的一条切线.
的图象的一条切线.
(1)求函数 的解析式及
的解析式及 的值;
的值;
(2)若 对于任意
对于任意 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)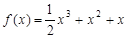 ,(2)
,(2)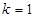 .
.
解析试题分析:(1) 先求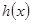 ,
,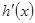 根据导数的几何意义,得:
根据导数的几何意义,得: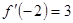 ,
, ,
,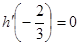 列方程,解得
列方程,解得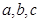 ,解得
,解得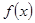 ,易知
,易知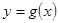 与
与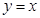 相交于
相交于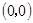 ,又相切,所以函数
,又相切,所以函数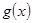 在原点处的切线斜率为1,即
在原点处的切线斜率为1,即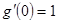 ,求出
,求出 ;(2)代入函数后,整理成
;(2)代入函数后,整理成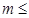
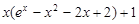 的形式,所以即求
的形式,所以即求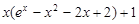 在
在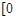 ,
, 的最小值,设
的最小值,设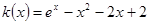 ,利用
,利用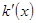 分析
分析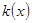 ,结合定义域,求出最小值.较难题型.
,结合定义域,求出最小值.较难题型.
试题解析:(1)解: , 1分
, 1分
由题意,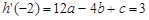 ,①
,①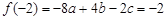 ,②
,②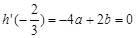 ,③
,③
由①②③解得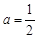 ,
,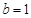 ,
,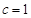 ,
,
所以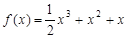 . 4分
. 4分
由题意, 与
与 相切可知,函数在原点处的切线斜率为1,
相切可知,函数在原点处的切线斜率为1,
因为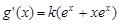 ,所以
,所以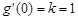 . 6分
. 6分
(2)解:问题等价于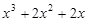
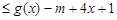 ,
,
整理得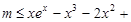
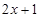 =
=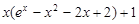 对于任意
对于任意 ,
, 恒成立,
恒成立,
只需求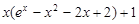 在
在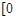 ,
, 的最小值. 8分
的最小值. 8分
设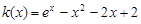 ,则
,则 , 10分
, 10分
又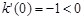 ,
,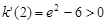 ,
,
所以 必有一实根
必有一实根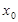 ,且
,且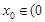 ,
,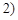 ,
,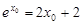 ,
,
当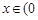 ,
,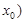 时,
时,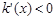 ;当
;当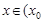 ,
, 时,
时,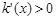 ,
,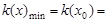
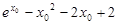
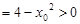 ,
,
所以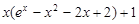 在
在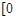 ,
, 的最小值为1, 13分
的最小值为1, 13分
所以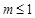 ,
,
即实数 的取值范围是
的取值范围是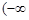 ,
,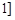 . 14分
. 14分
考点:1.导数的几何意义;2.利用导数求函数最值;3构造函数.

练习册系列答案
相关题目
 x2-
x2- 的取值范围.
的取值范围. +10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
+10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
 存在极大值和极小值,求
存在极大值和极小值,求 的取值范围;
的取值范围; 分别为
分别为 的极大值和极小值,其中
的极大值和极小值,其中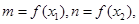 且
且 求
求 的取值范围.
的取值范围. 其中AF是以A为顶点、AD为对称轴的抛物线段.试求该高科技工业园区的最大面积.
其中AF是以A为顶点、AD为对称轴的抛物线段.试求该高科技工业园区的最大面积.
 ,
, .
. ,则
,则 ,
, 满足什么条件时,曲线
满足什么条件时,曲线 与
与 在
在 处总有相同的切线?
处总有相同的切线? 时,求函数
时,求函数 的单调减区间;
的单调减区间; 时,若
时,若 对任意的
对任意的 恒成立,求
恒成立,求