题目内容
15.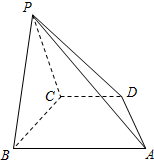 在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD.
在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD.(Ⅰ)求证:AB⊥平面PBC;
(Ⅱ)求平面ADP与平面BCP所成的锐二面角的大小.
分析 (Ⅰ)证明AB⊥平面PBC,利用面面垂直的性质,根据AB⊥BC,平面PBC⊥平面ABCD,即可得证;
(Ⅱ)取BC的中点O,连接PO,以O为原点,OB所在的直线为x轴,在平面ABCD内过O垂直于BC的直线为y轴,OP所在直线为z轴建立空间直角坐标系O-xyz,求出平面ADP与平面BCP的法向量,利用向量的夹角公式,即可求平面ADP与平面BCP所成的锐二面角的大小.
解答 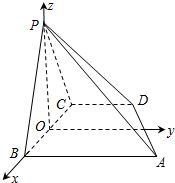 (Ⅰ)证明:因为∠ABC=90°,所以AB⊥BC,
(Ⅰ)证明:因为∠ABC=90°,所以AB⊥BC,
因为平面PBC⊥平面ABCD,平面PBC∩平面ABCD=BC,AB?平面ABCD,
所以AB⊥平面PBC.
(Ⅱ)解:如图,取BC的中点O,连接PO,
因为PB=PC,所以PO⊥BC.
因为PB=PC,所以PO⊥BC,
因为平面PBC⊥平面ABCD,所以PO⊥平面ABCD.
以O为原点,OB所在的直线为x轴,在平面ABCD内过O垂直于BC的直线为y轴,OP所在直线为z轴建立空间直角坐标系O-xyz.
不妨设BC=2.由AB=PB=PC=BC=2CD得,,
所以,
设平面PAD的法向量为=(x,y,z).
所以.
令x=-1,则,所以=(-1,2,).
取平面BCP的一个法向量,
所以cos<,>=,
所以平面ADP与平面BCP所成的锐二面角的大小为.
点评 本题考查线面垂直,考查平面ADP与平面BCP所成的锐二面角,解题的关键是掌握线面垂直的判定方法,正确运用向量法,属于中档题.

练习册系列答案
相关题目
6.已知一函数满足x>0时,有g′(x)=2x2>,则下列结论一定成立的是( )
| A. | -g(1)≤3 | B. | -g(1)≥2 | C. | -g(1)<4 | D. | -g(1)≥4 |
20.若函数f(x)=ax2+b|x|+c(a≠0)有四个单调区间,则实数a,b,c满足( )
| A. | b2-4ac>0,a>0 | B. | b2-4ac>0 | C. | ->0 | D. | -<0 |
7.已知二次函数f(x)的二次项系数为正数,且对任意x∈R,都有f(x)=f(4-x)成立,若f(1-2x2)<f(1+2x-x2),则实数x的取值范围是( )
| A. | (2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0) | D. | (-∞,-2)∪(0,+∞) |

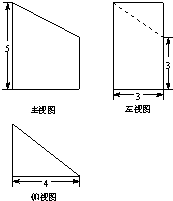
 如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点,N为AC中点.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点,N为AC中点. 如图,圆O的直径AB、BE为圆O的切线,点C为圆O上不同于A、B的一点,AD为∠BAC的平分线,且分别与BC交于H,与圆O交于D,与BE交于E,连结BD、CD.
如图,圆O的直径AB、BE为圆O的切线,点C为圆O上不同于A、B的一点,AD为∠BAC的平分线,且分别与BC交于H,与圆O交于D,与BE交于E,连结BD、CD.