题目内容
5.已知直线的极坐标方程为θ=$\frac{π}{4}$,它与曲线$\left\{\begin{array}{l}{x=1+2cosa}\\{y=2+2sina}\end{array}\right.$相交于A,B两点.〔1〕求︳AB|的大小;
〔2〕求过极坐标点〔2,$\frac{4π}{3}$〕,且与曲线相切的直线的直角坐标方程.
分析 (1)首先将极坐标方程和参数方程化为直角坐标方程,求出圆心到直线的距离,应用弦长公式l=2 $\sqrt{{r}^{2}-{d}^{2}}$求出弦长.
(2)把参数方程化为直角坐标方程,求出圆心和半径,分切线的斜率不存在、存在两种情况,分别求得切线的方程.
解答 解:(1)直线的极坐标方程为θ=$\frac{π}{4}$(ρ∈R),化为普通方程:y=x,
曲线$\left\{\begin{array}{l}x=1+2cosa\\ y=2+2sina\end{array}\right.$(α为参数),化为普通方程为:(x-1)2+(y-2)2=4,
其圆心为(1,2),半径r=2,
则圆心到直线的距离为d=$\frac{|1-2|}{\sqrt{2}}$=$\frac{1}{\sqrt{2}}$,
故弦长|AB|=2$\sqrt{{r}^{2}-{d}^{2}}$=2$\sqrt{4-\frac{1}{2}}$=$\sqrt{14}$.
(2)根据点M的极坐标点〔2,$\frac{4π}{3}$〕,可得点M的直角坐标为(-1,-$\sqrt{3}$),
把曲线C直角坐标方程为:(x-1)2+(y-2)2=4,
表示圆心为(1,2),半径r=2,
当切线的斜率不存在时,切线的方程为x=-1,
当切线的斜率存在时,设切线的方程为y+$\sqrt{3}$=k(x+1),即 kx-y-$\sqrt{3}$+k=0,
由圆心到切线的距离等于半径,$\frac{|2k-2-\sqrt{3}|}{\sqrt{1+{k}^{2}}}=2$可得 6k2-24k-13=0,求得k=$\frac{3+4\sqrt{3}}{8+4\sqrt{3}}$,
故切线的方程为 (3+3$\sqrt{3}$)x-(8+4$\sqrt{3}$)y+9+4$\sqrt{3}$=0,
综上可得,圆的切线方程为:(3+3$\sqrt{3}$)x-(8+4$\sqrt{3}$)y+9+4$\sqrt{3}$=0和x=-1,
点评 本题主要考查极坐标方程、参数方程与普通方程的互化,同时考查直线与圆相交的弦长公式.考查把参数方程化为直角坐标方程的方法,直线和圆相切的性质,点到直线的距离公式的应用,体现了分类讨论的数学思想.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案| A. | -10 | B. | -8 | C. | -6 | D. | -4 |
从甲、乙两个分厂生产的零件中各抽出500件,量其内径尺寸的结果如下表:
甲厂的零件内径尺寸:
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 15 | 30 | 125 | 198 | 77 | 35 | 20 |
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) | ||||
| 频数 | 40 | 70 | 79 | 162 | 59 | 55 | 35 | ||||
| 甲厂 | 乙厂 | 合计 | |
| 优质品 | |||
| 非优质品 | |||
| 合计 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.025 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
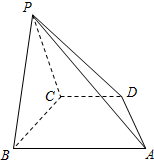 在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD.
在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD.