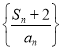题目内容
【题目】已知曲线C的极坐标方程是ρsin2θ-8cosθ=0.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系xOy.在直角坐标系中,倾斜角为α的直线l过点P(2,0).
(1)写出曲线C的直角坐标方程和直线l的参数方程;
(2)设点Q与点G的极坐标分别为![]() ,(2,π),若直线l经过点Q
,(2,π),若直线l经过点Q![]() ,且与曲线C相交于A,B两点,求△GAB的面积.
,且与曲线C相交于A,B两点,求△GAB的面积.
【答案】(1) y2=8x, ![]() (t为参数).(2)
(t为参数).(2) ![]() .
.
【解析】
(1)曲线C可化为ρ2sin2θ-8ρcosθ=0,即得其直角坐标方程,根据已知写出直线l的参数方程;(2)先求出直线l的参数方程为 ,将l的参数方程代入曲线C的直角坐标方程得到t2-8
,将l的参数方程代入曲线C的直角坐标方程得到t2-8![]() t-32=0,利用韦达定理和直线参数方程t的几何意义求出|AB|=16, 再求点G到直线l的距离,即得△GAB的面积.
t-32=0,利用韦达定理和直线参数方程t的几何意义求出|AB|=16, 再求点G到直线l的距离,即得△GAB的面积.
(1)曲线C可化为ρ2sin2θ-8ρcosθ=0,
其直角坐标方程为y2=8x,直线l的参数方程为![]() (t为参数).
(t为参数).
(2)将点![]() 的极坐标化为直角坐标得(0,-2),易知直线l的倾斜角α=
的极坐标化为直角坐标得(0,-2),易知直线l的倾斜角α=![]() ,
,
所以直线l的参数方程为 (t为参数).
(t为参数).
将l的参数方程代入曲线C的直角坐标方程,得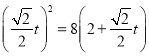 ,
,
整理得t2-8![]() t-32=0,Δ=(8
t-32=0,Δ=(8![]() )2+4×32=255>0,
)2+4×32=255>0,
设t1,t2为方程为t2-8![]() t-32=0的两个根,则t1+t2=8
t-32=0的两个根,则t1+t2=8![]() ,t1·t2=-32,
,t1·t2=-32,
所以![]() .
.
由极坐标与直角坐标互化公式得点G的直角坐标为(-2,0),易求点G到直线l的距离![]() ,所以
,所以![]() .
.

【题目】从某工厂的一个车间抽取某种产品50件,产品尺寸(单位:cm)落在各个小组的频数分布如下表:
数据分组 | [12.5,15.5) | [15.5,18.5) | [18.5,21.5) | [21.5,24.5) | [24.5,27.5) | [27.5,30.5) | [30.5,33.5) |
频数 | 3 | 8 | 9 | 12 | 10 | 5 | 3 |
(1)根据频数分布表,求该产品尺寸落在[27.5,33.5]内的概率;
(2)求这50件产品尺寸的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(3)根据频数分布对应的直方图,可以认为这种产品尺寸![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均值
近似为样本平均值![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() .利用该正态分布,求
.利用该正态分布,求![]() (
(![]() ).
).
附:(1)若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]()
![]() ;(2)
;(2)![]() .
.