Question

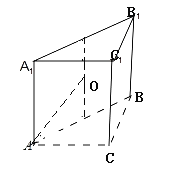
【题目】已知三棱柱ABC﹣A1B1C1的侧棱垂直于底面，各顶点都在同一球面上，若该棱柱的体积为，AB＝2，AC＝1，∠BAC＝60°，则此球的表面积等于（ ）

A.8πB.9πC.10πD.11π

Answer 1

【答案】A

【解析】

由AB＝2，AC＝1，∠BAC＝60°可得三角形ABC的面积及外接圆的半径，再由三棱柱ABC﹣A1B1C1的侧棱垂直于底面，所以三棱柱的外接球的球心是过底面外接圆的圆心作垂直于底面的直线与中截面的交点，可得外接球的半径，进而求出外接球的表面积．

由AB＝2，AC＝1，∠BAC＝60°，由余弦定理可得：

BC，

∴，∠ACB＝90°，∴底面外接圆的圆心在斜边AB的中点，

设三角形ABC的外接圆的半径为r，则r1，

又，

所以V柱＝S△ABCAA1，所以可得AA1＝2，

因为三棱柱ABC﹣A1B1C1的侧棱垂直于底面，

所以三棱柱的外接球的球心是过底面外接圆的圆心作垂直于底面的直线与中截面的交点，

设外接球的半径为R，则R2＝r2+（）2＝12+12＝2，

所以外接球的表面积S＝4πR2＝4π×2＝8π，

故选：A．