题目内容

i
，
j
是平面直角坐标系（坐标原点为O）内分别与x轴、y轴正方向相同的两个单位向量，且
OA
=4
i
+2
j
，
OB
=3
i
+4
j
，则△OAB的面积等于（　　）
A、15B、10C、7.5D、5
分析：本题求三角形的面积，根据题目条件有两边长度可求出，又两边的夹角可用向量法求出，故用公式S=
1
2
absinC求面积，由此知求解本题先用向量的模公式求两邻边的长度再由内积公式求两边的夹角．
解答：解：由已知：A（4，2），B（3，4）．
则
OA
•
OB
=12+8=20，|
OA
|=2
5
，|
OB
|=5．
∴cos∠AOB=
OA
•
OB
|
OA
||
OB
|
=
20
2
5
×5
=
2
5
5
，
∴sin∠AOB=
5
5
，
∴S△OAB=
1
2
|
OA
|•|
OB
|sin∠AOB
1
2
×2
5
×5
5
5
=5．
故应选D．
点评：本题考查向量数量积的运算，向量模的公式，三角形的面积公式，涉及到的知识点较多，综合性较强．
练习册系列答案
相关题目
设x、y∈R，
i
、
j
为直角坐标平面内x、y轴正方向上的单位向量，
a
=x
i
+（y+2）
j
，
b
=x
i
+（y-2）
j
，且|
a
|+|
b
|=8．
（1）求点M（x，y）的轨迹C的方程；
（2）过点（0，3）作直线l与曲线C交于A、B两点，设
OP
=
OA
+
OB
，是否存在这样的直线l，使得四边形OAPB是矩形？若存在，求出直线l的方程；若不存在，试说明理由．
设x，y∈R，
i
，
j
是直角坐标平面内x，y轴正方向上的单位向量，若
a
=x
i
+(y+3)
j
，
b
=x
i
+(y-3)
j
且|
a
|+|
b
|=6，则点M（x，y）的轨迹是（　　）

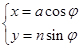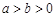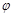在平面直角坐标系xoy中，曲线C1的参数方程为 (，为参数），在以O为极点，x轴的正半轴为极轴的极坐标系中，曲线C2是圆心在极轴上，且经过极点的圆．已知曲线C1上的点M(1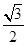，)对应的参数j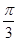＝，曲线C2过点D(1，)．

（I）求曲线C1，C2的直角坐标方程；

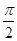（II）若点A(r1，q)，B(r2，q＋)在曲线C1上，求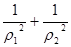的值．

 
设x、y∈R，
i
、
j
为直角坐标平面内x、y轴正方向上的单位向量，
a
=x
i
+（y+2）
j
，
b
=x
i
+（y-2）
j
，且|
a
|+|
b
|=8．
（1）求点M（x，y）的轨迹C的方程；
（2）过点（0，3）作直线l与曲线C交于A、B两点，设
OP
=
OA
+
OB
，是否存在这样的直线l，使得四边形OAPB是矩形？若存在，求出直线l的方程；若不存在，试说明理由．
设x，y∈R，i，j是直角坐标平面内x，y轴正方向的单位向量，若a=xi+(y+2)j，b=xi+(y-2)j，且|a|+|b|=8．

(Ⅰ)求点M(x，y)的轨迹C的方程；

(Ⅱ)过点(0，3)作直线l与曲线C交于A、B两点，设，是否存在这样的直线l，使，若存在，求出l的方程；若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网