题目内容
19.命题P:存在实数x,x2-2cx+c<0;命题Q:|x-1|-x+2c>0对任意x∈R恒成立.若P或Q为真,P且Q为假,试求c的取值范围.分析 关于命题P:存在实数x,x2-2cx+c<0,即存在实数x,使得(x-c)2<c2-c即可,只需c2-c>0,解得c范围.命题Q:|x-1|-x+2c>0,化为2c>x-|x-1|,令f(x)=x-|x-1|=$\left\{\begin{array}{l}{1,x≥1}\\{2x-1,x<1}\end{array}\right.$,可得f(x)≤1.即可得出c的取值范围.若P或Q为真,P且Q为假,P与Q必然一真一假.
解答 解:关于命题P:存在实数x,x2-2cx+c<0,
即存在实数x,使得(x-c)2<c2-c即可,
∴只需c2-c>0,解得:c<0或c>1,
∴P真:c<0或c>1;
命题Q:|x-1|-x+2c>0,
化为2c>x-|x-1|,
令f(x)=x-|x-1|=$\left\{\begin{array}{l}{1,x≥1}\\{2x-1,x<1}\end{array}\right.$,
∴f(x)≤1.
∴2c>1,解得c$>\frac{1}{2}$.
若P或Q为真,P且Q为假,
∴P与Q必然一真一假.
∴$\left\{\begin{array}{l}{c<0或c>1}\\{c≤\frac{1}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{0≤c≤1}\\{c>\frac{1}{2}}\end{array}\right.$,
解得c<0或$\frac{1}{2}>c≤1$.
因此c的取值范围是$(-∞,0)∪(\frac{1}{2},1]$.
点评 本题考查了一元二次不等式的解法、绝对值不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.已知$\overrightarrow{a}$=(0,-2$\sqrt{3}}$),$\overrightarrow b$=(1,$\sqrt{3}}$),则$\overrightarrow{a}$在$\overrightarrow b$上的正射影的数量为( )
| A. | $\sqrt{3}$ | B. | 3 | C. | -$\sqrt{3}$ | D. | -3 |
4.等差数列{an}、{bn}中的前n项和分别为Sn、Tn,$\frac{{S}_{n}}{{T}_{n}}$=$\frac{2n}{3n+1}$,则$\frac{{a}_{10}}{{b}_{10}}$=( )
| A. | $\frac{20}{31}$ | B. | $\frac{19}{29}$ | C. | $\frac{17}{28}$ | D. | $\frac{16}{27}$ |
8.下列各组中的函数相等的是( )
| A. | f(x)=$\sqrt{{x}^{2}}$,g(x)=($\sqrt{x}$)2 | B. | f(x)=|x|,g(x)=$\sqrt{{t}^{2}}$ | ||
| C. | f(x)=$\frac{{x}^{2}-1}{x-1}$,g(x)=x+1 | D. | f(x)=$\sqrt{x+1}-\sqrt{x-1}$,g(x)=$\sqrt{{x}^{2}-1}$ |
9.有一个几何体的三视图及其尺寸如图(单位:cm),则该几何体的体积为( )
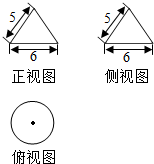

| A. | 12πcm3 | B. | 15πcm3 | C. | 24πcm3 | D. | 36πcm3 |