题目内容
11.已知函数f(x)=sin(2x+$\frac{π}{6}$).(1)求函数f(x)的单调递增区间:
(2)若直线x=t(t∈(0,$\frac{π}{2}$)既是函数y=f(x)图象的对称轴又是函数g(x)=sin2x+acos2x图象的对称轴,求实数a的值.
分析 (1)由条件利用正弦函数的单调性求得函数f(x)的单调递增区间.
(2)由条件求得t=$\frac{π}{6}$,再根据直线x=t=$\frac{π}{6}$ 是函数g(x)=sin2x+acos2x的图象的对称轴,可得g(0)=g($\frac{π}{3}$),由此求得a的值.
解答 解:(1)对于函数f(x)=sin(2x+$\frac{π}{6}$),令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,
求得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,可得函数的增区间为[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z.
(2)由直线x=t(t∈(0,$\frac{π}{2}$)既是函数y=f(x)图象的对称轴,可得2t+$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,
即t=$\frac{kπ}{2}$+$\frac{π}{6}$,k∈Z,∴t=$\frac{π}{6}$.
再根据直线x=t=$\frac{π}{6}$ 是函数g(x)=sin2x+acos2x 的图象的对称轴,
可得g(0)=g($\frac{π}{3}$),即0+a=$\frac{\sqrt{3}}{2}$-$\frac{1}{2}$a,求得a=$\frac{\sqrt{3}}{3}$.
点评 本题主要考查正弦函数的图象特征,正弦函数的单调性以及图象的对称性,属于中档题.

练习册系列答案
相关题目
6.邵东某桶装水经营部每天的房租、人员工资等固定成本为360元,每桶水进价4元,销售单价与日均销量的关系如表所示
请根据以上数据作出分析,这个经营部怎样定价(单价要为整元)才能获得最大利润?最大利润为多少?
| 销售单价/元 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 日均销售量/桶 | 360 | 320 | 280 | 240 | 200 | 160 | 120 |
20.下列等式成立的是( )
| A. | log2[(-3)(-5)]=log2(-3)+log2(-5) | B. | log2(-10)2=2log2(-10) | ||
| C. | log2[(-3)(-5)]=log23+log25 | D. | log2(-5)3=-log253 |
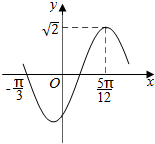 函数f(x)=$\sqrt{2}$sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为f(x)=$\sqrt{2}$sin(2x+$\frac{π}{6}$);f(x)的图象的横坐标缩小为原来的$\frac{1}{2}$后得函数y=g(x)的图象,则g(x)的单调减区间为[$\frac{π}{12}$+$\frac{1}{2}$kπ,$\frac{π}{3}$+$\frac{1}{2}$kπ],k∈Z.
函数f(x)=$\sqrt{2}$sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为f(x)=$\sqrt{2}$sin(2x+$\frac{π}{6}$);f(x)的图象的横坐标缩小为原来的$\frac{1}{2}$后得函数y=g(x)的图象,则g(x)的单调减区间为[$\frac{π}{12}$+$\frac{1}{2}$kπ,$\frac{π}{3}$+$\frac{1}{2}$kπ],k∈Z.