题目内容
若不等式组
表示的区域面积为S,则
(1)当S=2时,k=
;
(2)当k>1时,
的最小值为
|
(1)当S=2时,k=
| 1 |
| 4 |
| 1 |
| 4 |
(2)当k>1时,
| kS |
| k-1 |
32
32
.分析:(1)根据题意,可得直线l:y=-kx+4k与x、y的正半轴分别交于点A(4,0),B(0,4k),进而得到不等式表示的平面区域是图中△AOB,结合题意建立关于k的方程并解之,即可得到实数k的值;
(2)结合(1)的计算,可得
=
,其中k>1.然后利用配凑的方法,结合基本不等式求最值,得当且仅当k=2时,
的最小值为32.
(2)结合(1)的计算,可得
| kS |
| k-1 |
| 8k2 |
| k-1 |
| kS |
| k-1 |
解答:解:(1)∵直线l:y=-kx+4k=-k(x-4)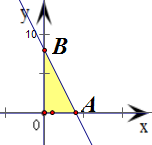
∴直线l经过点A(4,0),令x=0,得y=4k,直线l交y轴于点B(0,4k)
因此,不等式组
表示的区域是图中△AOB,
其面积为S=
×|OA|×|OB|=8k=2,解之得k=
;
(2)由(1),得S=8k,可得
=
=
,其中k>1
=8(k-1)+
+16,
∵8(k-1)+
≥2
=16
∴当且仅当8(k-1)=
时,即k=2时,8(k-1)+
的最小值为16,
由此可得
≥16+16=32,即k>1时,
的最小值为32
故答案为:
,32

∴直线l经过点A(4,0),令x=0,得y=4k,直线l交y轴于点B(0,4k)
因此,不等式组
|
其面积为S=
| 1 |
| 2 |
| 1 |
| 4 |
(2)由(1),得S=8k,可得
| kS |
| k-1 |
| k(8k) |
| k-1 |
| 8k2 |
| k-1 |
| 8k2 |
| k-1 |
| 8 |
| k-1 |
∵8(k-1)+
| 8 |
| k-1 |
8(k-1)×
|
∴当且仅当8(k-1)=
| 8 |
| k-1 |
| 8 |
| k-1 |
由此可得
| 8k2 |
| k-1 |
| kS |
| k-1 |
故答案为:
| 1 |
| 4 |
点评:本题给出二元一次不等式组表示的平面区域,求与区域面积有关的一个最小值,着重考查了简单线性规划及其应用和二元一次不等式的处理等知识,属于基础题.

练习册系列答案
相关题目
若不等式组
表示的平面区域是一个三角形,则s的取值范围是( )
|
| A、s≥4 |
| B、0<s≤2 |
| C、2≤s≤4 |
| D、0<s≤2或s≥4 |